题目内容
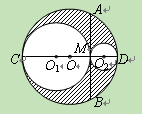
(2011•恩施州)如图,已知AB为⊙O的直径,BD为⊙O的切线,过点B的弦BC⊥OD交⊙O于点C,垂足为M.
(1)求证:CD是⊙O的切线;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值)
(1)求证:CD是⊙O的切线;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值)

(1)证明:连接OC
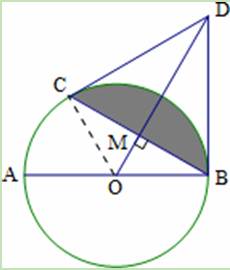
∵OD⊥BC,O为圆心,
∴OD平分BC.
∴DB=DC.
∴△OBD≌△OCD.(SSS)
∴∠OCD=∠OBD.
又∵AB为⊙O的直径,BD为⊙O的切线,
∴∠OCD=∠OBD=90°,
∴CD是⊙O的切线;
(2)∵DB、DC为切线,B、C为切点,
∴DB=DC.
又DB=BC=6,
∴△BCD为等边三角形.
∴∠BOC=360°﹣90°﹣90°﹣60°=120°,
∠OBM=90°﹣60°=30°,BM=3.
∴OM= ,OB=2
,OB=2 .
.
∴S阴影部分=S扇形OBC﹣S△OBC
=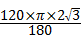 ﹣
﹣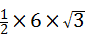
=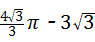 (cm2).
(cm2).

∵OD⊥BC,O为圆心,
∴OD平分BC.
∴DB=DC.
∴△OBD≌△OCD.(SSS)
∴∠OCD=∠OBD.
又∵AB为⊙O的直径,BD为⊙O的切线,
∴∠OCD=∠OBD=90°,
∴CD是⊙O的切线;
(2)∵DB、DC为切线,B、C为切点,
∴DB=DC.
又DB=BC=6,
∴△BCD为等边三角形.
∴∠BOC=360°﹣90°﹣90°﹣60°=120°,
∠OBM=90°﹣60°=30°,BM=3.
∴OM=
 ,OB=2
,OB=2 .
.∴S阴影部分=S扇形OBC﹣S△OBC
=
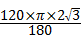 ﹣
﹣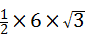
=
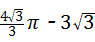 (cm2).
(cm2).略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目

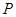 的正上方
的正上方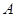 处,从
处,从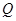 ,若∠
,若∠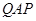 =
=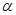 ,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( ) 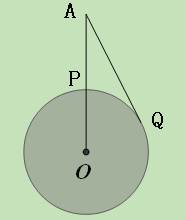
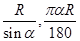
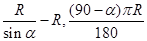
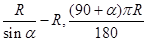
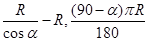
 cm,
cm, cm
cm cm
cm
 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作

 内接于⊙
内接于⊙ ,若
,若 =30°,
=30°, ,则⊙
,则⊙

 ).
).