题目内容
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
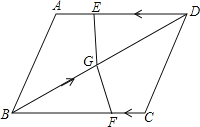
(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
【答案】(1)见解析;(2)共有三次,移动的时间分别为1秒、2.4秒、4秒、4.2秒,
移动的距离分别为4、7.5、7.5、7.2.
【解析】
试题分析:(1)由AD=BC=12,AB=CD,BD为公共边,所以可证得△ABD≌△CDB,所以可知∠ADB=∠CBD,所以AD∥BC;
(2)设运动时间为t,设G点的移动距离为y,根据全等三角形的性质进行解答即可.
(1)证明:在△ABD和△CDB中,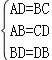 ,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,
∴AD∥BC,
(2)解:设G点的移动距离为y,
∵AD∥BC,
∴∠EDG=∠FBG,
若△DEG与△BFG全等,
则有△DEG≌△BFG或△DGE≌△BFG,
可得:DE=BF,DG=BG;或DE=BG,DG=BF,
①当E由D到A,
即0<t≤3时,有4t=12﹣t,解得:t=2.4,
∵y=15﹣y,
∴y=7.5,
或4t=y,解得:t=1,
∵12﹣t=15﹣y,∴y=4,
②当F由A返回到D,即3<t≤6时,有24﹣4t=12﹣t,解得:t=4,
∵y=15﹣y,∴y=7.5,
或24﹣4t=y,解得:t=4.2
∵12﹣t=15﹣y,y=7.2,
综上可知共有三次,移动的时间分别为1秒、2.4秒、4秒、4.2秒,
移动的距离分别为4、7.5、7.5、7.2.