题目内容
【题目】如图,Rt△ABC中,∠C=90°、∠A=30°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论正确的序号是 (多填或错填得0分,少填酌情给分).
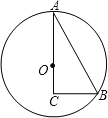
①AO=2CO;
②AO=BC;
③以O为圆心,以OC为半径的圆与AB相切;
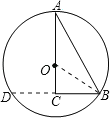
④延长BC交⊙O与D,则A、B、D是⊙O的三等分点.
【答案】①③④
【解析】
试题分析:连接OB,可得∠ABO=30°,则∠OBC=30°,根据直角三角形的性质得OC=![]() OB=
OB=![]() OA,再根据三角函数cos∠OBC=
OA,再根据三角函数cos∠OBC=![]() ,则BC=
,则BC=![]() OB,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长,根据垂径定理得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分.
OB,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长,根据垂径定理得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分.
解:连接OB,∴OA=OB,
∴∠A=∠ABO,
∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∴∠OBC=30°,
∴OC=![]() OB=
OB=![]() OA,
OA,
即OA=2OC,
故①正确;
∵cos∠OBC=![]() ,
,
∴BC=![]() OB,
OB,
即BC=![]() OA,
OA,
故②错误;
∵∠ABO=∠OBC=30°,
∴点O在∠ABC的角平分线上,
∴点O到直线AB的距离等于OC的长,
即以O为圆心,以OC为半径的圆与AB相切;
故③正确;
延长BC交⊙O于D,
∵AC⊥BD,
∴AD=AB,
∴△ABD为等边三角形,
∴![]() =
=![]() =
=![]() ,
,
∴点A、B、D将⊙O的三等分.
故④正确.
故答案为①③④.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目