题目内容
【题目】如果∠A是锐角,则下列结论正确个数为( )个.
①![]() =sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
=sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
A.1
B.2
C.3
D.4
【答案】C
【解析】解: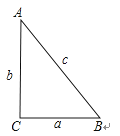
∵在Rt△ACB中,∠C=90°,AC=b,BC=a,AB=c,如图,
sinA=![]() , cosA=
, cosA=![]() , tanA=
, tanA=![]() ,
,
∴![]() =1﹣sinA,sinA+cosA=
=1﹣sinA,sinA+cosA=![]() +
+![]() =
=![]() >1,tanA>sinA,
>1,tanA>sinA,
∵cosA=![]() , sin(90°﹣∠A)=sinB=
, sin(90°﹣∠A)=sinB=![]() ,
,
∴cosA=sin(90°﹣∠A),
即正确的有②③④,共3个,
故选C.
【考点精析】根据题目的已知条件,利用同角三角函数的关系(倒数、平方和商)的相关知识可以得到问题的答案,需要掌握各锐角三角函数之间的关系:平方关系(sin2A+cos2A=1);倒数关系(tanAtan(90°—A)=1);弦切关系(tanA=sinA/cosA ).

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目