题目内容
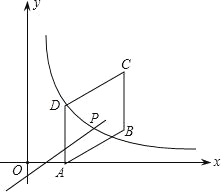
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3-3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3-3k的图象经过点C,当x>![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3-3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是![]() <a<3.
<a<3.
其中正确的是( )
A.①③ B.②③ C.②④ D.③④
【答案】D.
【解析】
试题解析:①∵四边形ABCD是平行四边形,
∴AD=BC,
∵B(6,2),C(6,6),
∴BC⊥x轴,AD=BC=4,
而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,
,
∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3-3k=6k+3-3k=3k+3≠6,
∴一次函数y=kx+3-3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3-3k的图象经过点C,
∴6=6k+3-3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得: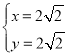 或
或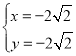 (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3-3k(k≠0),y随x的增大而增大,
∴k>0,
∴交点P在第一象限,
∴点P横坐标a的取值范围是![]() <a.
<a.
将x=3带入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
又∵一次函数y2=kx+3-3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,
)的左方,
∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.