题目内容
【题目】三个小球上分别标有数字﹣2,﹣1,3,它们除数字外其余全部相同,现将它们放在一个不透明的袋子里,从袋子中随机地摸出一球,将球上的数字记录,记为m,然后放回;再随机地摸取一球,将球上的数字记录,记为n,这样确定了点(m,n).
(1)请列表或画出树状图,并根据列表或树状图写出点(m,n)所有可能的结果;
(2)求点(m,n)在函数y=﹣ ![]() 的图象上的概率.
的图象上的概率.
【答案】
(1)解:由题意可得,
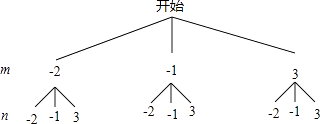
点(m,n)的所有可能结果是:(﹣2,﹣2)、(﹣2,﹣1)、(﹣2,3)、(﹣1,﹣2)、(﹣1,﹣1),(﹣1,3)、(3,﹣2)、(3、﹣1)、(3,3)
(2)解:∵点(m,n)的所有可能结果是:(﹣2,﹣2)、(﹣2,﹣1)、(﹣2,3)、(﹣1,﹣2)、(﹣1,﹣1),(﹣1,3)、(3,﹣2)、(3、﹣1)、(3,3),
∴点(﹣2,3)、(3,﹣2)在函数y=﹣ ![]() 的图象上,
的图象上,
∴点(m,n)在函数y=﹣ ![]() 的图象上的概率是
的图象上的概率是 ![]()
【解析】(1)根据题意可以画出树状图,从而可以写出点(m,n)的所有可能性;(2)根据(1)中点(m,n)的所有可能性可以得到哪几个点在函数y=﹣ ![]() 的图象上,从而可以求得点(m,n)在函数y=﹣
的图象上,从而可以求得点(m,n)在函数y=﹣ ![]() 的图象上的概率.
的图象上的概率.
【考点精析】掌握列表法与树状图法是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.

【题目】如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则 ①DE=DF;②DF=EF;③△DCF≌△DGE;④EF= ![]() .
.
上面结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【题目】小明用下面的方法求出方程2 ![]() ﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
2 | 令 | t= | t= |
|
x﹣2 | ||||
x+2+ |



