题目内容
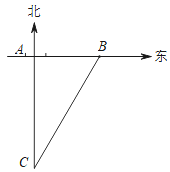
【题目】如图，甲、乙两人在道路的两边相向而行，当甲、乙两人分别行至点A、C时，测得乙在甲的北偏东60°方向上．乙留在原地休息，甲继续向前走了40米到B处，此时测得乙在其北偏东30°方向上．求道路的宽（参考数据：
）
【答案】道路的宽约为34.64米.
【解析】
过C作AB的垂线，设垂足为D．易知∠BAC=30°，∠PBD=60°．∠BCA=∠BAC=30°，得CB=AB=40米；在Rt△BCD中，可用正弦函数求出DC的长．
过点C作CD⊥AB于点D，则CD的长即为道路的宽.
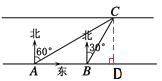
由题意得∠CAD=30°，∠CBD=60°.
∵∠CBD是△ACB的一个外角，
∴∠ACB=∠CBD-∠CAB=30°．
∴∠CAB=∠ACB，
故AB=PB=40(m)．
在Rt△BCD中，∠BDC=90°，∠CBD=60°，CB=40m，
∴CD=CBsin60°=40×
=20
≈34.64(米)．
∴道路的宽约为34.64米.
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
