题目内容
【题目】如图1,在![]() ABC中,
ABC中,![]() ,
,![]() ,点D是AB中点,
,点D是AB中点,

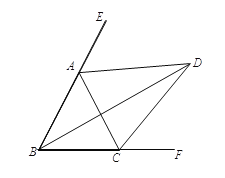
(1)点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.
(i)求证:△BCD为等边三角形;
(ii)随着点E位置的变化,![]() 的度数是否变化?若不变化,求出
的度数是否变化?若不变化,求出![]() 的度数;
的度数;
(2)DP![]() AB交AC于点P,点E为线段AP上一点,连结BE,作
AB交AC于点P,点E为线段AP上一点,连结BE,作![]() ,如图2所示,EQ交PD延长线于Q,探究线段PE,PQ与AP之间的数量关系,并证明.
,如图2所示,EQ交PD延长线于Q,探究线段PE,PQ与AP之间的数量关系,并证明.
【答案】(1)(i)见解析;(ii)∠DBF的度数不变,∠DBF=30°;(2) PQ=AP+ PE,证明见解析.
【解析】
(1)(i)由∠C=90°、∠A=30°,可得出AB=2BC、∠CBD=60°,根据直角三角形斜边上的中线定理可得出BD=BC,即可得出△BCD为等边三角形;
(ii)由(i)可得出∠ECD=30°,根据∠BDC=∠EDF=60°可得出∠BDF=∠CDE,再结合BD=CD、DF=DE即可得出△BDF≌△CDE(SAS),根据全等三角形的性质即可得出∠DBF=∠DCE=30°,即∠DBF的度数不变;
(2)连接BP,延长BP至F,使PF=PE,连接EF,证出△PEF为等边三角形,得出PF=PE=EF,∠F=∠EPF=60°,得到∠F=∠BPQ=60°,证出∠Q=∠EBF,由AAS证明△BEF≌△QEP,得出PQ=FB=BP+PF=BP+PE,证出AP=BP,即可得出结论.
解:(1)(i)∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC,∠CBD=60°.
∵点D是AB中点,
∴BD=BC,
∴△BCD为等边三角形;
(ii)∠DBF的度数不变,
∵∠ACB=90°,点D是AB中点,
∴CD=![]() AB=AD,
AB=AD,
∴∠ECD=30°.
∵△BDC为等边三角形,
∴BD=DC,∠BDC=60°.
又∵△DEF为等边三角形,
∴DF=DE,∠FDE=60°,
∴∠BDC +∠FDC=∠FDE+∠FDC,
∴∠BDF=∠CDE.
在△BDF和△CDE中,
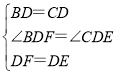 ,
,
∴△BDF≌△CDE(SAS),
∴∠DBF=∠DCE=30°,
即∠DBF的度数不变,∠DBF=30°;
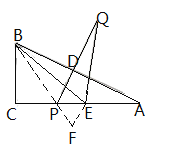
(2) PQ=AP+ PE,理由如下:
连接BP,延长BP至F,使PF=PE,连接EF,如图所示:
∵在![]() ABC中,
ABC中,![]() ,
,![]() ,点D是AB中点,DP
,点D是AB中点,DP![]() AB,
AB,
∴AP=BP,∠ABP=∠A=30°,
∵∠FPE=∠A+∠ABP=30°+30°=60°,
∴△PEF为等边三角形,
∴PF=PE=EF,∠F=60°,
∵∠APQ=90°∠A=60°,
∴∠F=∠QPE=60°,
∴∠BPQ=180°∠APQ∠FPE=60°,
∴∠BPQ=∠BEQ=60°,
∴∠Q=∠EBF,
在△BEF和△QEP中,
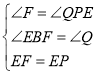
∴△BEF≌△QEP,
∴PQ=FB=BP+PF,
∵AP=BP,PE=PF,
∴PQ=AP+ PE.

 应用题作业本系列答案
应用题作业本系列答案