题目内容
【题目】已知,如图,在△ABC 中,AD 平分∠BAC,AD=AB,CM⊥AD 于 M,请你通过观察和测量,猜想线段 AB、AC 之和与线段 AM 有怎样的数量关系,并证明你的结论.
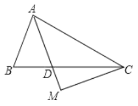
【答案】AB+AC=2AM.证明见解析
【解析】
根据题目提供的条件和图形中线段的关系,做出猜想AB+AC=2AM,过点C作CE∥AB,CE与AM的延长线交于点E,进一步证明AB+AC=AB+CE=AD+ED=AE,从而得到AB+AC=2AM.
猜想:AB+AC=2AM.
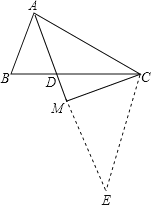
证明:过点C作CE∥AB,CE与AM的延长线交于点E.
则∠ECD=∠B,∠E=∠BAD.
(两直线平行,内错角相等)
∵AD平分∠BAC,∴∠BAD=∠CAD.
(角平分线定义)
∴∠E=∠CAD.(等量代换)
∴AC=EC.(等角对等边)
又CM⊥AD于M,
∴AM=ME,即AE=2AM.
(等腰三角形底边上的高线与底边上的中线重合)
∵AD=AB,∴∠B=∠ADB.(等边对等角)
又∠EDC=∠ADB,(对顶角相等)∴∠ECD=∠EDC.(等量代换)
∴ED=EC.(等角对等边)
∴AB+AC=AB+CE=AD+ED=AE.(等量代换)
∴AB+AC=2AM.

练习册系列答案
相关题目