Question

【题目】尺规作图：作线段AB的垂直平分线MN，并证明该作图所得到的MN就是线段AB的垂直平分线.

Answer 1

【答案】见解析.

【解析】

分别以A、B为圆心，以大于AB为半径画弧，两弧交于两点，过这两点作直线即可；根据作法和图形，写出已知求证，再利用△AMN≌△BMN得出△AMB是等腰三角形，进而得出MN⊥AB，MN平分AB．

解：如图，直线MN即为所求；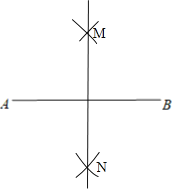

作法：（1）分别以A、B为圆心，大于AB的同样长为半径作弧，两弧分别交于点M、N；
（2）作直线MN．
直线MN即为所求作的线段AB的垂直平分线；

已知：如图，连接AM、BM、AN、BN，AM=AN=BM=BN．
求证：MN⊥AB，MN平分AB．
证明：设MN与AB交于点O．

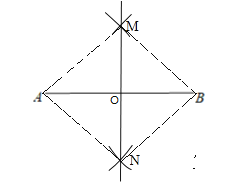
∵在△AMN和△BMN中，

，
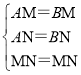∴△AMN≌△BMN（SSS）．
∴∠AMN =∠BMN．
∵AM=BM，
∴△AMB是等腰三角形．
∴MO⊥AB，AO=BO．
即MN⊥AB，MN平分AB．