题目内容
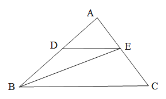
【题目】已知：在△ABC中，点D、点E分别在边AB、AC上，且DE // BC，BE平分∠ABC．
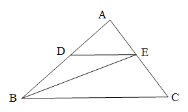
（1）求证：BD=DE；
（2）若AB=10，AD=4，求BC的长．
【答案】（1）见解析；（2）15
【解析】
（1）利用平行线性质及角平分线线定理得到∠DEB=∠DBE，再利用等腰三角形判定得到BD=DE ，即得到答案.
（2）利用相似的判定得到△ADE∽△ABC，再利用相似的性质得到
，代入值即可得到答案.
（1）证明： ∵DE // BC，
∴∠DEB=∠EBC
∵ BE平分∠ABC
∴∠DBE=∠EBC
∴∠DEB=∠DBE
∴BD=DE
(2) 解：∵AB=10，AD=4
∴BD=DE=6
∵DE // BC
∴△ADE∽△ABC
∴
∴
∴BC=15
练习册系列答案
相关题目
