题目内容
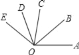
【题目】如图,已知OB平分∠AOC,OD平分∠COE,∠AOD=110°,∠BOE=100°,求∠AOE的度数.
【答案】140°
【解析】
设∠EOD=∠DOC=x°,求出∠AOB=∠COB=100°-2x°,根据∠AOD=110°得出方程,求出x的值,即可求出.
解:∵OB平分∠AOC,OD平分∠COE,
∴设∠EOD=∠DOC=x°,∠AOB=∠COB,
∵∠AOD=110°,∠BOE=100°,
∴∠AOB=∠BOC=100°﹣2x°,
∴∠COD+∠COB+∠AOB=110°,
∴x+100﹣2x+100﹣2x=110,
解得x=30,
即∠EOD=∠DOC=30°,
∴∠AOE=∠AOD+∠DOE=110°+30°=140°.

练习册系列答案
相关题目