Question

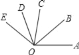
【题目】如图，O是直线AB上一点，OC平分∠AOB，在直线AB另一侧，以O为顶点作∠DOE＝90°.

(1)若∠AOE＝48°，则∠BOD＝______，∠AOE与∠BOD的关系是_______；

(2)∠AOE与∠COD有什么关系？请写出你的结论，并说明理由．

Answer 1

【答案】（1）42°，互余；（2）∠AOE与∠COD互补，理由见解析

【解析】

（1）结合图形，根据平角的定义可求得∠BOD的度数，再根据余角的定义即可得∠AOE与∠BOD的关系；

（2）根据补角的定义即可得∠AOE与∠COD的关系.

(1) ∵∠AOE+∠DOE+∠BOD=180°，∠AOE=48°，∠DOE=90°，

∴∠BOD=180°-48°-90°=42°，

∴∠AOE+∠BOD=48°+42°=90°，

即∠AOE与∠BOD互余，

故答案为：42°，互余；

(2)∠AOE与∠COD互补，理由如下：

∵OC平分∠AOB，∴∠COB＝90°，

∵∠DOE＝90°，∴∠AOE＋∠BOD＝90°，

∴∠AOE＋∠COD＝∠AOE＋∠BOD＋∠COB＝90°＋90°＝180°，

∴∠AOE与∠COD互补.