题目内容
【题目】如图,⊙A,⊙B的半径分别为1cm,2cm,圆心距AB为5cm.如果⊙A由图示位置沿直线AB向右平移2cm,则此时该圆与⊙B的位置关系是( )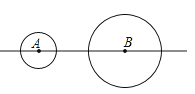
A.外离
B.相交
C.外切
D.内含
【答案】C
【解析】解答:∵圆心距AB是5cm,把⊙A由图示位置沿直线AB向右平移2cm,
∴新的圆心距AB是5-2=3cm,
又∵⊙A和⊙B的半径分别是1cm和2cm,则2-1=1,2+1=3,
∴两圆恰好外切.故选C.
求出把⊙A由图示位置沿直线AB向右平移2cm后,⊙A和⊙B的圆心距,再求出两圆半径的和与差,与该圆心距进行比较,确定两圆的位置关系.
【考点精析】认真审题,首先需要了解圆与圆的位置关系(两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.).

练习册系列答案
相关题目
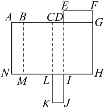
【题目】如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?