题目内容
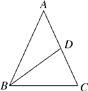
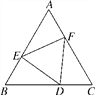
【题目】如图,在△ABC中,∠B=∠C,点D为BC边上(B,C点除外)的动点,∠EDF的两边与AB,AC分别交于点E,F,且BD=CF,BE=CD.
(1)求证:DE=DF;
(2)若∠EDF=m,用含m的代数式表示∠A的度数;
(3)连接EF,求当△DEF为等边三角形时∠A的度数.
【答案】(1)见解析;(2)180°-2m;(3)60°.
【解析】(1)利用SAS证明△BDE≌△CFD,再根据全等三角形的对应边相等即可得;
(2)由△BDE≌△CFD,可得∠BDE=∠CFD,再根据平角定义可得以及三角形内角和可得∠EDF=∠C,结合∠A+∠B+∠C=180°,∠B=∠C即可推得∠A=180°-2m;
(3)由△DEF为等边三角形,可得m=60°,继而可求得∠A=60°.
(1)在△BDE与△CFD中,
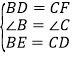 ,
,
∴△BDE≌△CFD,
∴DE=DF;
(2)∵△BDE≌△CFD,∴∠BDE=∠CFD,
∵∠BDE+∠EDF+∠CDF=180°,
∴∠EDF+∠CDF+∠CFD=180°,
∵∠C+∠CDF+∠CFD=180°,∴∠EDF=∠C,
∵∠A+∠B+∠C=180°,∠B=∠C,∴∠A+2∠EDF=180°,
∴∠A=180°-2∠EDF,即∠A=180°-2m;
(3)∵△DEF为等边三角形,∴m=60°,
∴∠A=180°-2×60°=60°.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目