题目内容
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。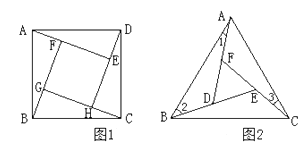
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设 ![]() ,
, ![]() ,
, ![]() ,请探索
,请探索 ![]() ,
, ![]() ,
, ![]() 满足的等量关系。
满足的等量关系。
【答案】
(1)
△ABD≌△BCE≌△CAF.
证明: ∵正△ABC中,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,又∠2=∠3
∴∠ABD=∠BCE,
又∵∠1=∠2,
∴△ABD≌△BCE(ASA).

(2)
△DEF是正三角形.
证明:∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形.
(3)
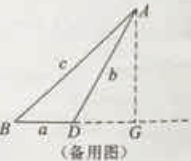
解:作AG⊥BD,交BD延长线于点G.
由△DEF是正三角形得到∠ADG=60°(或者∠ADG=∠1+∠ABD=∠2+∠ABD=60°.)
∴在Rt△ADG中,DG=![]() b,AG=
b,AG=![]() b.
b.
∴在Rt△ABG中,c2=![]() +
+![]() ,
,
∴c2=a2+ab+b2
【解析】(1)由正△AB得出∠CAB=∠ABC=∠BCA=60°,AB=BC,再通过等量代换得出∠1=∠2,从而得出△ABD≌△BCE(ASA).
(2)由(1)中△ABD≌△BCE≌△CAF,得出∠ADB=∠BEC=∠CFA,∠FDE=∠DEF=∠EFD,从而得出△DEF是正三角形.
(3)作AG⊥BD,交BD延长线于点G.由△DEF是正三角形得到∠ADG=60°(或者∠ADG=∠1+∠ABD=∠2+∠ABD=60°.)从而在Rt△ADG中,
DG=![]() b,AG=
b,AG=![]() b;在Rt△ABG中,c2=
b;在Rt△ABG中,c2=![]() +
+![]() ,最后得出c2=a2+ab+b2
,最后得出c2=a2+ab+b2
【考点精析】通过灵活运用含30度角的直角三角形和勾股定理的概念,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

【题目】柯桥区某企业因为发展需要,从外地调运来一批94吨的原材料,现有甲、乙、丙三种车型共选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费6400元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?