题目内容
已知函数y1=x，y2=（x+1）2-7．
（1）求它们图象的交点；
（2）结合图象，确定当x为何值时，有y1＞y2；y1＜y2？
（1）求它们图象的交点；
（2）结合图象，确定当x为何值时，有y1＞y2；y1＜y2？
（1）解方程组
得
，
．
所以直线y1=x与抛物线y2=（x+1）2-7的交点是（2，2）和（-3，-3）．
（2）观察函数）y1=x与y2=（x+1）2-7的图象
由图象可知：当-3＜x＜2时，有y1＞y2，
当x＞2或x＜-3时，有y1＜y2．
|
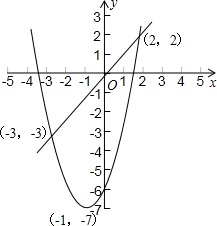
得
|
|
所以直线y1=x与抛物线y2=（x+1）2-7的交点是（2，2）和（-3，-3）．
（2）观察函数）y1=x与y2=（x+1）2-7的图象
由图象可知：当-3＜x＜2时，有y1＞y2，
当x＞2或x＜-3时，有y1＜y2．
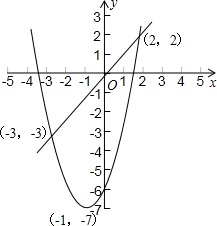
练习册系列答案
相关题目
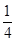x2+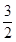
x－2交x轴于A，B两点（点A在点B的左侧），交y轴于点C，分别过点B，C作y轴，x轴的平行线，两平行线交于点D，将△BDC绕点C逆时针旋转，使点D旋转到y轴上得到△FEC，连接BF．