题目内容
如图,抛物线y=-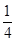 x2+
x2+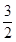 x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
(1)求点B,C所在直线的函数解析式;
(2)求△BCF的面积;
(3)在线段BC上是否存在点P,使得以点P,A,B为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

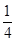 x2+
x2+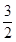 x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.(1)求点B,C所在直线的函数解析式;
(2)求△BCF的面积;
(3)在线段BC上是否存在点P,使得以点P,A,B为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

(1)直线BC的解析式为y=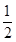 x﹣3;
x﹣3;
(2)△BCF的面积为10;
(3)在线段BC上存在点P,使得以点P,A,B为顶点的三角形与△BOC相似, P点坐标为(2,﹣1)或( ,﹣
,﹣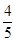 ).
).
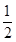 x﹣3;
x﹣3;(2)△BCF的面积为10;
(3)在线段BC上存在点P,使得以点P,A,B为顶点的三角形与△BOC相似, P点坐标为(2,﹣1)或(
 ,﹣
,﹣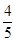 ).
).试题分析:(1)根据坐标轴上点的坐标特征可得点B,C的坐标,再根据待定系数法可得点B,C所在直线的函数解析式;
(2)根据勾股定理可得BC的长,根据旋转的性质和三角形面积公式即可求解;
(3)存在.分两种情况讨论:①过A作AP1⊥x轴交线段BC于点P1,则△BAP1∽△BOC;②过A作AP2⊥BC,垂足点P2,过点P2作P2Q⊥x轴于点Q.则△BAP2∽△BCO;依此讨论即可求解.
试题解析:(1)当y=0时,﹣
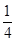 x2+
x2+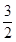 x﹣2=0,
x﹣2=0,解得x1=2,x2=4,
∴点A,B的坐标分别为(2,0),(4,0),
当x=0时,y=﹣2,
∴C点的坐标分别为(0,﹣2),
设直线BC的解析式为y=kx+b(k≠0),则
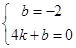 ,
,解得
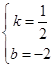 .
.∴直线BC的解析式为y=
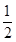 x﹣3;
x﹣3;(2)∵CD∥x轴,BD∥y轴,
∴∠ECD=90°,
∵点B,C的坐标分别为(4,0),(0,﹣2),
∴BC=
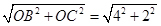 =2
=2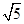 ,
,∵△FEC是由△BDC绕点C逆时针旋转得到,
∴△BCF的面积=
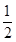 BC•FC=
BC•FC=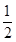 ×2
×2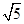 ×2
×2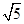 =10;
=10;(3)存在.分两种情况讨论:
①过A作AP1⊥x轴交线段BC于点P1,则△BAP1∽△BOC,
∵点A的坐标为(2,0),
∴点P1的横坐标是2,
∵点P1在点BC所在直线上,
∴y=
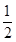 x﹣2=
x﹣2=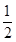 ×2﹣2=﹣1,
×2﹣2=﹣1,∴点P1的坐标为(2,﹣1);
②过A作AP2⊥BC,垂足点P2,过点P2作P2Q⊥x轴于点Q.

∴△BAP2∽△BCO,
∴
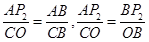 ,
,∴
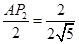 ,
,解得AP2=
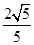 ,
,∵
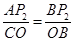 ,
,∴AP2•BP=CO•BP2,
∴
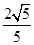 ×4=2BP2,
×4=2BP2,解得BP2=
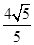 ,
,∵
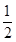 AB•QP2=
AB•QP2=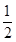 AP2•BP2,
AP2•BP2,∴2QP2=
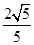 ×
×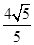 ,
,解得QP2=
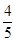 ,
,∴点P2的纵坐标是﹣
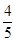 ,
,∵点P2在BC所在直线上,
∴x=
 ,
,∴点P2的坐标为(
 ,﹣
,﹣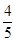 ),
),∴满足条件的P点坐标为(2,﹣1)或(
 ,﹣
,﹣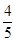 ).
).
练习册系列答案
相关题目
 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.

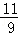 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案? x+m与抛物线y=
x+m与抛物线y= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;
