��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr���������¶��壺����P�ĺᡢ�������Ϊ�������ҵ�Բ��C�ľ���d��r�����PΪ��C �Ĺ�������.
��1������O�İ뾶r=2ʱ���ڵ�D��2��-2����E��-1��0����F��0��2���У�Ϊ��O�Ĺ���������� ��
��2����ֱ��![]() �ϴ��ڡ�O�Ĺ������㣬�Ҳ�����7������r��ȡֵ��Χ��
�ϴ��ڡ�O�Ĺ������㣬�Ҳ�����7������r��ȡֵ��Χ��
��3����C��Բ����x���ϣ��뾶Ϊ2����ֱ��![]() �ϴ��ڡ�C�Ĺ������㣬��Բ��C�ĺ�����t��ȡֵ��Χ.
�ϴ��ڡ�C�Ĺ������㣬��Բ��C�ĺ�����t��ȡֵ��Χ.
���𰸡���1��E��F ����2��![]() �� r ��
�� r ��![]() ����3��
����3��![]() ��t��
��t��![]() .
.
��������
��1�����ݹ�������Ķ�������жϼ���.
��2���������ֱ��![]() ����һ����O�Ĺ�������ʱ������O����G��2,2��ʱ���뾶r��ֵ�������ֱ��
����һ����O�Ĺ�������ʱ������O����G��2,2��ʱ���뾶r��ֵ�������ֱ��![]() ����9����O�Ĺ�������ʱ������O����L��-2,6��ʱ���뾶r��ֵ���������.
����9����O�Ĺ�������ʱ������O����L��-2,6��ʱ���뾶r��ֵ���������.
��3���ֱ��������C����M��3,1���͡�C����N��5,-1��ʱ��Բ��C�ĺ����꼴��.
��1����D,E,F�ĺᡢ�������Ϊ��������D��Բ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �������������Ķ���.
�������������Ķ���.
��E��Բ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �����������Ķ���.
�����������Ķ���.
��F��Բ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �����������Ķ���.
�����������Ķ���.
��E,FΪ��O�Ĺ�������
�ʴ�Ϊ��E��F ��
��2������O����G��2,2��ʱ��r=![]() ��
��
��O����L��-2,6��ʱ��r=![]() ��
��
��![]() �� r ��
�� r ��![]()
��3����ͼ��ʾ��
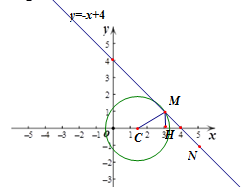
����C����M��3,1��ʱ��CM=2��MH=1��
��CH=![]() ����ʱ��C�ĺ�����t=
����ʱ��C�ĺ�����t=![]() ��
��
����C����N��5,-1��ʱ����C�ĺ�����t=![]() ��
��
��![]() ��t��
��t��![]() .
.

����Ŀ����������ˮ���깺��һ����ˮ��������Ϊ 10 Ԫ/ǧ�ˣ��ۼ۲����� 10 Ԫ/ǧ�ˣ��Ҳ����� 16 Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ��������� y��ǧ���� �������ۼ� x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ
������ y��ǧ�ˣ� | �� | 29 | 28 | 27 | 26 | �� |
�ۼ� x��Ԫ/ǧ�ˣ� | �� | 10.5 | 11 | 11.5 | 12 |
��1��ij������ˮ�����ۼ�Ϊ 14 Ԫ/ǧ�ˣ������ˮ������������
��2�����ij����������ˮ������ 100 Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��