Question

【题目】如图 1，长方形 ABCD 中，AB＝3cm，BC＝6cm，P 为矩形 ABCD 上的动点，动点 P 从 A 出发，沿着 A-B-C-D 运动到 D 点停止，速度为 1cm/s，设点 P 运动时间为 x 秒，△APD 的面积为 ycm.

（1）填空:①当 x＝6 时，对应 y 的值为________；9≤x＜12 时，y 与 x 之间的关系式为_____；

（2）当 y＝3 时，求 x 的值；

（3）当 P 在线段 BC 上运动时，是否存在点 P 使得△APD 的周长最小？若存在，求出此时∠APD 的度数；若不存在，请说明理由.

图1

Answer 1

【答案】 9 y＝-3x＋36

【解析】（1）利用三角形面积求法S△APD＝即可得出答案；当9＜x≤12时，点P运动到CD边上，S△APD＝得出y与x的函数关系式即可；

（2）分别求出点P在AB、BC、CD上y与x的函数关系式，利用y＝3，求出x的值即可；

（3）利用轴对称求最短路线的方法得出P点位置，进而利用全等三角形的性质求出答案．

（1）9；y＝-3x＋36；

（2）当 P 从 A-B 运动时，y＝3x；当 P 从 B-C 运动时，y＝9；当 P 从 C-D 运动时，y＝-3x＋36；令 y＝3，则 3x＝3 或-3x＋36＝3，解得 x＝1 或 11.

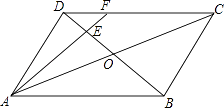
（3）存在.理由：如图，延长 DC，使得 DC＝D’C，连接 AD’，交 BC 于点 P，则 P 为所求，

且△PCD≌△PCD’，

∴PD＝PD’，∠PCD＝∠PCD’ 因为四边形 ABCD 是长方形

∴AB＝CD,∠B＝∠PCD＝90°

∴AB＝CD’，∠PCD’＝90°

在△ABP 与△D’CP 中，

∴△ABP≌△D’CP（AAS）

∴BP PCBC3，

∵AB＝DC＝3，

∴AB＝BP，PC＝CD，

∴∠APB＝∠BAP＝45°，∠DPC＝∠DPC＝45°，

∵∠APB＋∠APD＋∠CPD＝180°，

∴∠APD＝90°.