题目内容
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
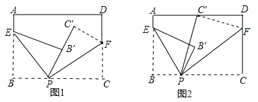
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
【答案】(1)90°;(2)85°
【解析】分析:(1)由对称性得到两对角相等,而这两对角之和为180°,利用等量代换及等式的性质即可求出折痕的夹角∠EPF的度数;
(2)由对称性得到两对角相等,根据题意得到这两对角之和为190°,利用等量代换及等式的性质即可求出∠EPF的度数.
详解:(1)由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF.
∵∠BPE+∠B′PE+∠CPF+∠C′PF=180°,∴∠EPF=∠B′PE+∠C′PF=![]() ×180°=90°;
×180°=90°;
(2)由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF.
∵∠BPE+∠B′PE+∠CPF+∠C′PF=180°+10°=190°,∴∠BPE+∠CPF=95°,∴∠FPE=85°.

【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)