Question

如图，平面直角坐标系的单位是厘米，直线AB的解析式为y=x－6，分别与x 轴y轴相交于A、B 两点．动点C从点B出发沿射线BA以3cm/秒的速度运动，以C点为圆心作半径为1cm的⊙C．

（1）求A、B两点的坐标；
（2）设⊙C运动的时间为t，当⊙C和坐标轴相切时，求时间t的值．
（3）在点C运动的同时，另有动点P以2cm/秒的速度在线段OA上来回运动，过点P作直线l垂直于x轴．若点C与点P同时分别从点B、点O开始运动，求直线l与⊙C所有相切时点P的坐标．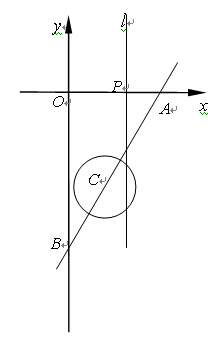

Answer 1

（1）A（6,0），B（0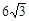，）  ……各1分，共2分
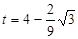（2）  综上t= 或或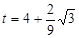
（3）    

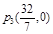
解析试题分析：（1）根据直线方程分别令x，y值为零，即可得出B，A坐标．
（2）分圆与y轴、x轴两种相切情况进行讨论．
（3）直线与圆第二次相交共有两次，分别算出四次的相交时的时间，然后算出C点坐标．
考点：一次函数综合题．
点评：本题重点为分析出直线和圆何时相切，分情况讨论．相切是有交点的临界点．