题目内容
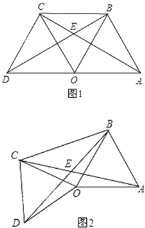
【题目】如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.
(1)证明:⊿ABC ≌ ⊿DCB;
(2)求∠AEB的大小.
(3)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【答案】(1)详见解析;(2)60° (3)60°
【解析】
(1)利用题中信息可得:![]() 都为等边三角形,找出它们之间的等量关系去证明全等;
都为等边三角形,找出它们之间的等量关系去证明全等;
(2)根据等边三角形和外角的性质,可求![]() ;
;
(3)方法同上,只是![]() ,此时已不是外角,但仍可用外角和内角的关系解答.
,此时已不是外角,但仍可用外角和内角的关系解答.
证明:(1)
![]() ,且
,且![]() 都为等边三角形,
都为等边三角形,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
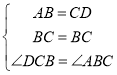 ,
,
![]() ;
;
(2)如图所示:
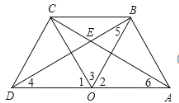
![]() 和
和![]() 都是等边三角形,
都是等边三角形,
且点O是线段![]() 的中点,
的中点,
![]() ,∠
,∠![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
同理![]() ,
,
![]()
![]() .
.
(3)如图所示:
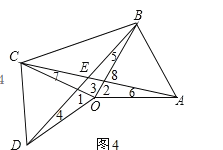
![]() 都是等边三角形,
都是等边三角形,
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]()
![]()

练习册系列答案
相关题目
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.