题目内容
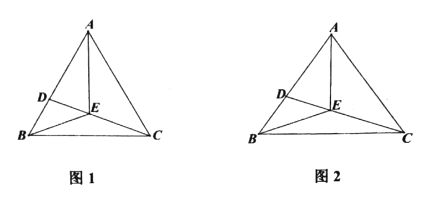
【题目】如图,点![]() 为等边三角形
为等边三角形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,以
,以![]() 为一边作
为一边作![]() ,且
,且![]() ,连接
,连接![]() 、
、![]() .
.
(1)判断![]() 与
与![]() 的大小关系并证明;
的大小关系并证明;
(2)若![]() ,
,![]() ,
,![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
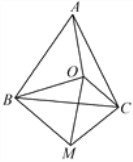
【答案】(1)AO=CM,见解析;(2)△OMC是直角三角形,见解析.
【解析】
(1)可证出△OBM是等边三角形,得出OM=OB=BM,由∠ABC=∠OBM得出∠ABO=∠CBM,根据SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
解:(1)AO=CM;理由如下:
∵∠OBM=60°,OB=BM,
∴ △OBM是等边三角形
∴ OM=OB=BM,
∠ABC=∠OBM=60°
∴∠ABO=∠CBM,
在△AOB和△CMB中,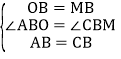 ,
,
∴△AOB≌△CMB(SAS),
∴ AO=CM;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,
∴OM2=OC2+CM2,
∴△OMC是直角三角形.
故答案为:(1)AO=CM,见解析;(2)△OMC是直角三角形,见解析.

练习册系列答案
相关题目