Question

【题目】完成下列各题：

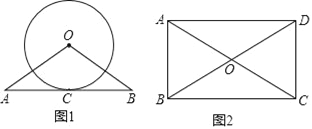
（1）如图，已知直线AB与⊙O相切于点C，且AC=BC，求证：OA=OB．

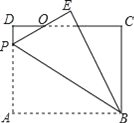
（2）如图，矩形ABCD的两条对角线相交于点O，∠AOD=120°，AB=3，求AC的长．

Answer 1

【答案】（1）证明见解析；（2）6cm

【解析】试题分析：（1）根据线段垂直平分线的性质：线段垂直平分线上的点到两端点的距离相等来证明；

（2）根据矩形性质得出AC=BD，OA=OB，求出∠AOB=60°，得出△AOB是等边三角形，求出∠ADB=30°，得出AC=BD=2AB=6cm即可．

（1）证明：连接OC，

∵直线AB与⊙O相切于点C，

∴OC⊥AB，

又∵AC=BC，

∴OC垂直平分AB，

∴OA=OB；

（2）证明：∵四边形ABCD是矩形，

∴AC=BD，OA=OC=AC，BO=DO=BD，∠BAD=90°，

∴OA=OB，

∵∠AOD=120°，

∴∠AOB=60°，

∴△AOB是等边三角形，

∴∠ABO=60°，∠ADB=30°，

∴AC=BD=2AB=6cm．