Question

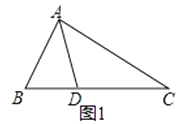
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，BE是中线，CG平分∠ACB交BE于点G，F为AB边上一点，且∠ACF=∠CBG．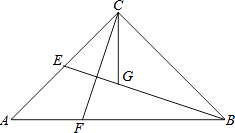

（1）求证：CF=BG；
（2）延长CG交AB于点H，判断点G是否在线段AB的垂直平分线上？并说明理由．
（3）过点A作AD⊥AB交BE的延长线于点D，请证明：CF=2DE．

Answer 1

【答案】
（1）证明：∵∠ACB=90°，AC=BC，

∴∠A=∠ABC=45°，

∵CG平分∠ACB，

∴∠BCG=45°=∠A，

∴∠BCG=∠CAB=45°，

在△ACF和△BCG中， ，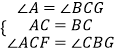

∴△ACF≌△BCG（ASA），

∴AF=CG，CF=BG

（2）解：点G在线段AB的垂直平分线上，如图1所示：理由如下：

∵AC=BC，CG平分∠ACB，

∴CH⊥AB，H为AB中点，

∴点G在线段AB的垂直平分线上

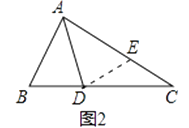
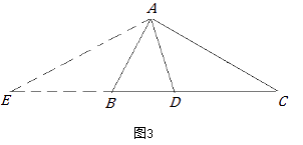
（3）证明：连接AG．如图2所示：

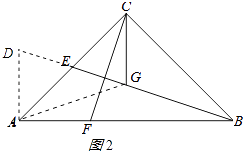
由（2）可知，AG=BG，∠GAB=∠GBA，

∵AD⊥AB，

∴∠GAB+∠GAD=∠GBA+∠D=90°，

∴∠GAD=∠D，

∴GA=GD=GB=CF．

∵AD⊥AB，CH⊥AB

∴CH∥AD，

∴∠D=∠EGC，

∵E为AC中点，

∴AE=EC，

在△AED和△CEG中， ，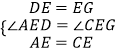

∴△AED≌△CEG（SAS），

∴DE=EG，

∴DG=2DE，

∴CF=2DE

【解析】（1）根据角平分线的性质、等边对等角和已知条件证明出△ACF≌△BCG，得出AF=CG，CF=BG；（2）根据等腰三角形的三线合一，得到点G在线段AB的垂直平分线上；（3）由（2）可知，AG=BG，∠GAB=∠GBA，已知AD⊥AB，得到∠GAD=∠D，GA=GD=GB=CF，得到 △AED≌△CEG，得到DE=EG，DG=2DE，CF=2DE.