题目内容
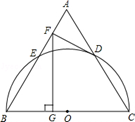
如图MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,

(1)在MN上找一点P,使PA+PC最短;
(2)求出PA+PC最短的距离。

(1)在MN上找一点P,使PA+PC最短;
(2)求出PA+PC最短的距离。
(1)作出点P见解析;(2) .
.
 .
.试题分析:(1)根据已知条件圆的直径等于10,
 ,已知AE=4,CF=3,首先做出点A关于直径MN的对称点G点,可知点G也在圆上,连接对称点G和点C,那么与直径MN的交点,即为点P,那么也可以作点C关于直径的的对称点,同样也可以得到点P;(2)要求PA+PC的最短距离,根据(1)中的结论和题中条件如果点P在圆心,那么线段就是最短的,解决问题的关键在于题中AE=4,CF=3,再连接OA,OC,根据勾股定理和相似三角形的性质,即可得到线段相等,得到最短距离
,已知AE=4,CF=3,首先做出点A关于直径MN的对称点G点,可知点G也在圆上,连接对称点G和点C,那么与直径MN的交点,即为点P,那么也可以作点C关于直径的的对称点,同样也可以得到点P;(2)要求PA+PC的最短距离,根据(1)中的结论和题中条件如果点P在圆心,那么线段就是最短的,解决问题的关键在于题中AE=4,CF=3,再连接OA,OC,根据勾股定理和相似三角形的性质,即可得到线段相等,得到最短距离试题解析:(1)首先作出点A关于MN的对称点G,连接GC,那么与MN的交点即为P点,此时PA+PC最短;

(2)根据(1)中结论可知,PA=PG,连接OA,OC,
在直角三角形AEO和COF,中,分别求得:OE=3,OF=4,
在
 和
和 中,可到
中,可到
可得到PE=5,PF=3再结合勾股定理可知

所以PA+PC最短的距离为


练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
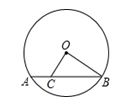
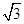 ,点C在弦AB上,AC=
,点C在弦AB上,AC=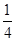 AB,则OC的长为( )
AB,则OC的长为( )