题目内容
抛物线T:y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,顶点在不同的位置,其图象构成“抛物线系”.
(1)抛物线T:y=x2+4x+4是否属于这个抛物线系?
(2)设抛物线T1与y轴交于点A,顶点C在x轴上,若抛物线T2:y=(x-2a)2+(a-1)(a<1)的顶点B到C的距离为2
,T2与y轴交于点D,在抛物线T1上是否存在点E,使四边形BCED为菱形?若存在.求出点E的坐标;若不存在,说明理由.
(3)在(2)中E不变的条件下,设抛物线T2向上平移得到抛物线T3,设抛物线T3与y轴交于点F,抛物线T2向上平移多少个单位,可使得∠FEC=45°?
(1)抛物线T:y=x2+4x+4是否属于这个抛物线系?
(2)设抛物线T1与y轴交于点A,顶点C在x轴上,若抛物线T2:y=(x-2a)2+(a-1)(a<1)的顶点B到C的距离为2
| 5 |
(3)在(2)中E不变的条件下,设抛物线T2向上平移得到抛物线T3,设抛物线T3与y轴交于点F,抛物线T2向上平移多少个单位,可使得∠FEC=45°?
考点:二次函数综合题
专题:压轴题
分析:(1)先求出抛物线T的顶点坐标所在的直线,然后求出抛物线y=x2+4x+4的顶点坐标,代入直线解析式验证即可进行判断;
(2)根据x轴上点的纵坐标为0求出a的值,从而求出点C的坐标,再求出点B的坐标,从而得到抛物线T2的解析式并求出点D的坐标,利用勾股定理列式求出BC=BD,过点D作DE∥BC,过点C作CE∥BD相交于点E,然后求出直线DE、CE的解析式,联立求解得到点E的坐标,再代入抛物线T1进行验证即可;
(3)连接AE,过点E作EG⊥x轴于G,可得四边形AEGO是正方形,延长EC交y轴于点H,连接OE,根据正方形的对角线平分一组对角可得∠FOE=45°,从而得到∠FOE=∠FEC,然后利用两组角对应相等两三角形相似求出△FEO和△FHO相似,根据相似三角形对应边成比例列式求出EF2=FO•FH,设FO=m,根据勾股定理表示出EF2,然后列出方程求解得到m,再求出FD的长度,即可得到平移距离.
(2)根据x轴上点的纵坐标为0求出a的值,从而求出点C的坐标,再求出点B的坐标,从而得到抛物线T2的解析式并求出点D的坐标,利用勾股定理列式求出BC=BD,过点D作DE∥BC,过点C作CE∥BD相交于点E,然后求出直线DE、CE的解析式,联立求解得到点E的坐标,再代入抛物线T1进行验证即可;
(3)连接AE,过点E作EG⊥x轴于G,可得四边形AEGO是正方形,延长EC交y轴于点H,连接OE,根据正方形的对角线平分一组对角可得∠FOE=45°,从而得到∠FOE=∠FEC,然后利用两组角对应相等两三角形相似求出△FEO和△FHO相似,根据相似三角形对应边成比例列式求出EF2=FO•FH,设FO=m,根据勾股定理表示出EF2,然后列出方程求解得到m,再求出FD的长度,即可得到平移距离.
解答:解:(1)设抛物线y=(x-2a)2+(a-1)的顶点坐标为(x,y),
则
,
消掉a得,y=
x-1,
∵y=x2+4x+4=(x+2)2,
∴y=x2+4x+4的顶点坐标为(-2,0),
当x=-2时,y=
×(-2)-1=-2≠0,
∴y=x2+4x+4不属于这个抛物线系;
(2)∵顶点C在x轴上,
∴a-1=0,
解得a=1,
∴C(2,0),
设点B(x,
x-1),
∵BC=2
,
∴(x-2)2+(
x-1)2=(2
)2,
整理得,x2-4x-12=0,
解得x1=-2,x2=6(舍去),
∴点B(-2,-2),
∴T2:y=(x+2)2-2,
令x=0,则y=(0+2)2-2=2,
∴点D(0,2),
∴BD=
=2
,
∴BC=BD,
过点D作DE∥BC,过点C作CE∥BD相交于点E,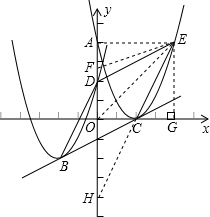
易求直线DE的解析式为y=
x+2,
设直线BD的解析式为y=kx+b,
则
,
解得
,
∴直线BD的解析式为y=2x+2,
易求直线CE的解析式为y=2x-4,
联立
,
解得
,
∴四边形BCED为菱形时点E(4,4),
当x=4时,T1:y=(4-2)2=4,
∴点E(4,4)在抛物线T1上,
故,抛物线T1上存在点E(4,4),使四边形BCED为菱形;
(3)连接AE,过点E作EG⊥x轴于G,
∵E(4,4),
∴四边形AEGO是正方形,
延长EC交y轴于点H,连接OE,
则∠FOE=45°,
∴∠FOE=∠FEC,
又∵∠EFO=∠HFE,
∴△FEO∽△FHO,
∴
=
,
∴EF2=FO•FH,
设FO=m,则AF=4-m,
由勾股定理得,EF2=(4-m)2+42,
∴(4-m)2+42=m(m+4),
解得m=
,
∴向上平移
-2=
个单位.
则
|
消掉a得,y=
| 1 |
| 2 |
∵y=x2+4x+4=(x+2)2,
∴y=x2+4x+4的顶点坐标为(-2,0),
当x=-2时,y=
| 1 |
| 2 |
∴y=x2+4x+4不属于这个抛物线系;
(2)∵顶点C在x轴上,
∴a-1=0,
解得a=1,
∴C(2,0),
设点B(x,
| 1 |
| 2 |
∵BC=2
| 5 |
∴(x-2)2+(
| 1 |
| 2 |
| 5 |
整理得,x2-4x-12=0,
解得x1=-2,x2=6(舍去),
∴点B(-2,-2),
∴T2:y=(x+2)2-2,
令x=0,则y=(0+2)2-2=2,
∴点D(0,2),
∴BD=
| (-2-0)2+(-2-2)2 |
| 5 |
∴BC=BD,
过点D作DE∥BC,过点C作CE∥BD相交于点E,

易求直线DE的解析式为y=
| 1 |
| 2 |
设直线BD的解析式为y=kx+b,
则
|
解得
|
∴直线BD的解析式为y=2x+2,
易求直线CE的解析式为y=2x-4,
联立
|
解得
|
∴四边形BCED为菱形时点E(4,4),
当x=4时,T1:y=(4-2)2=4,
∴点E(4,4)在抛物线T1上,
故,抛物线T1上存在点E(4,4),使四边形BCED为菱形;
(3)连接AE,过点E作EG⊥x轴于G,
∵E(4,4),
∴四边形AEGO是正方形,
延长EC交y轴于点H,连接OE,
则∠FOE=45°,
∴∠FOE=∠FEC,
又∵∠EFO=∠HFE,
∴△FEO∽△FHO,
∴
| EF |
| HF |
| FO |
| EF |
∴EF2=FO•FH,
设FO=m,则AF=4-m,
由勾股定理得,EF2=(4-m)2+42,
∴(4-m)2+42=m(m+4),
解得m=
| 8 |
| 3 |
∴向上平移
| 8 |
| 3 |
| 2 |
| 3 |
点评:本题是二次函数综合题型,主要利用了抛物线的顶点坐标的求解,菱形的性质,二次函数图象上点的坐标特征,相似三角形的判顶与性质,(2)根据平行直线的解析式的k值相等求出菱形的顶点E的坐标是解题的关键,(3)难点在于作辅助线构造出相似三角形.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
三角形的重心是三条( )的交点.
| A、高线 | B、角平分线 |
| C、中线 | D、以上都不对 |
 列方程(组)解应用题:
列方程(组)解应用题: