ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣAΓΔB «≈ΉΈοœΏy=ax2Θ®aΘΨ0Θ©…œΝΫΗω≤ΜΆ§ΒΡΒψΘ§Τδ÷–A‘ΎΒΎΕΰœσœόΘ§B‘ΎΒΎ“ΜœσœόΘ§
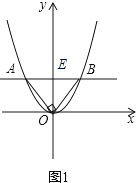
Θ®1Θ©»γΆΦ1Υυ ΨΘ§Β±÷±œΏAB”κx÷αΤΫ––Θ§ΓœAOB=90ΓψΘ§«“AB=2 ±Θ§«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΚΆAΓΔBΝΫΒψΒΡΚαΉχ±ξΒΡ≥ΥΜΐΘ°
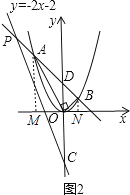
Θ®2Θ©»γΆΦ2Υυ ΨΘ§‘Ύ1Υυ«σΒΟΒΡ≈ΉΈοœΏ…œΘ§Β±÷±œΏAB”κx÷α≤ΜΤΫ––Θ§ΓœAOB»‘ΈΣ90Γψ ±Θ§AΓΔBΝΫΒψΒΡΚαΉχ±ξΒΡ≥ΥΜΐ «ΖώΈΣ≥Θ ΐΘΩ»γΙϊ «Θ§«κΗχ”η÷ΛΟςΘΜ»γΙϊ≤Μ «Θ§«κΥΒΟςάμ”…Θ°
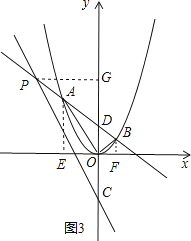
Θ®3Θ©‘Ύ2ΒΡΧθΦΰœ¬Θ§»τ÷±œΏy=©¹2x©¹2Ζ÷±πΫΜ÷±œΏABΘ§y÷α”ΎΒψPΓΔCΘ§÷±œΏABΫΜy÷α”ΎΒψDΘ§«“ΓœBPC=ΓœOCPΘ§«σΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΓΨΫβ¥πΓΩΫβΘΚ»γΆΦ1Θ§ΓΏAB”κx÷αΤΫ––Θ§
ΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ–‘”–AE=BE=1Θ§
ΓΏΓœAOB=90ΓψΘ§
ΓύOE=![]() AB=1Θ§
AB=1Θ§
ΓύAΘ®©¹1Θ§1Θ©ΓΔBΘ®1Θ§1Θ©Θ§
Α―x=1 ±Θ§y=1¥ζ»κy=ax2ΒΟΘΚa=1Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω Ϋy=x2Θ§
AΓΔBΝΫΒψΒΡΚαΉχ±ξΒΡ≥ΥΜΐΈΣxAxB=©¹1
Θ®2Θ©
xAxB=©¹1ΈΣ≥Θ ΐΘ§
»γΆΦ2Θ§ΙΐAΉςAMΓΆx÷α”ΎMΘ§BNΓΆx÷α”ΎNΘ§
ΓύΓœAMO=ΓœBNO=90ΓψΘ§
ΓύΓœMAO+ΓœAOM=ΓœAOM+ΓœBON=90ΓψΘ§
ΓύΓœMAO=ΓœBONΘ§
ΓύΓςAMOΓΉΓςBONΘ§
Γύ![]() Θ§
Θ§
ΓύOMON=AMBNΘ§
…ηAΘ®xAΘ§yAΘ©Θ§BΘ®xBΘ§yBΘ©Θ§
ΓΏAΘ®xAΘ§yAΘ©Θ§BΘ®xBΘ§yBΘ©‘Ύy=x2ΆΦœσ…œΘ§
ΓύΘ§yA=![]() Θ§yB=
Θ§yB=![]() Θ§
Θ§
Γύ©¹xAxB=yAyB=![]()
![]() Θ§
Θ§
ΓύxAxB=©¹1ΈΣ≥Θ ΐΘΜ
Θ®3Θ©
…ηAΘ®mΘ§m2Θ©Θ§BΘ®nΘ§n2Θ©Θ§
»γΆΦ3Υυ ΨΘ§ΙΐΒψAΓΔBΖ÷±πΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣEΓΔFΘ§‘ρ“Ή÷ΛΓςAEOΓΉΓςOFBΘ°
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§’ϊάμΒΟΘΚmnΘ®mn+1Θ©=0Θ§
Θ§’ϊάμΒΟΘΚmnΘ®mn+1Θ©=0Θ§
ΓΏmnΓΌ0Θ§Γύmn+1=0Θ§Φ¥mn=©¹1Θ°
…η÷±œΏABΒΡΫβΈω ΫΈΣy=kx+bΘ§ΝΣΝΔ![]() Θ§ΒΟΘΚx2©¹kx©¹b=0Θ°
Θ§ΒΟΘΚx2©¹kx©¹b=0Θ°
ΓΏmΘ§n «ΖΫ≥ΧΒΡΝΫΗωΗυΘ§Γύmn=©¹bΘ°
Γύb=1Θ°
ΓΏ÷±œΏAB”κy÷αΫΜ”ΎΒψDΘ§‘ρOD=1Θ°
“Ή÷ΣCΘ®0Θ§©¹2Θ©Θ§OC=2Θ§ΓύCD=OC+OD=3Θ°
ΓΏΓœBPC=ΓœOCPΘ§ΓύPD=CD=3Θ°
…ηPΘ®aΘ§©¹2a©¹2Θ©Θ§ΙΐΒψPΉςPGΓΆy÷α”ΎΒψGΘ§‘ρPG=©¹aΘ§GD=OG©¹OD=©¹2a©¹3Θ°
‘ΎRtΓςPDG÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚPG2+GD2=PD2Θ§
Φ¥ΘΚΘ®©¹aΘ©2+Θ®©¹2a©¹3Θ©2=32Θ§’ϊάμΒΟΘΚ5a2+12a=0Θ§
ΫβΒΟa=0Θ®…α»ΞΘ©Μρa=![]() Θ§
Θ§
Β±a=![]() ±Θ§©¹2a©¹2=
±Θ§©¹2a©¹2=![]() Θ§
Θ§
ΓύPΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩΘ®1Θ©»γΆΦ1Θ§”…AB”κx÷αΤΫ––Θ§ΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ–‘”–AE=BE=1Θ§”…”ΎΓœAOB=90ΓψΘ§ΒΟΒΫOE=![]() AB=1Θ§«σ≥ωAΘ®©¹1Θ§1Θ©ΓΔBΘ®1Θ§1Θ©Θ§Α―x=1 ±Θ§y=1¥ζ»κy=ax2ΒΟΘΚa=1ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω Ϋy=x2 Θ§ AΓΔBΝΫΒψΒΡΚαΉχ±ξΒΡ≥ΥΜΐΈΣxAxB=©¹1
AB=1Θ§«σ≥ωAΘ®©¹1Θ§1Θ©ΓΔBΘ®1Θ§1Θ©Θ§Α―x=1 ±Θ§y=1¥ζ»κy=ax2ΒΟΘΚa=1ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω Ϋy=x2 Θ§ AΓΔBΝΫΒψΒΡΚαΉχ±ξΒΡ≥ΥΜΐΈΣxAxB=©¹1
Θ®2Θ©»γΆΦ2Θ§ΙΐAΉςAMΓΆx÷α”ΎMΘ§BNΓΆx÷α”ΎNΒΟΒΫΓœAMO=ΓœBNO=90ΓψΘ§÷Λ≥ωΓςAMOΓΉΓςBONΘ§ΒΟΒΫOMON=AMBNΘ§…ηAΘ®xA Θ§ yAΘ©Θ§BΘ®xB yBΘ©Θ§”…”ΎAΘ®xA Θ§ yAΘ©Θ§BΘ®xB Θ§ yBΘ©‘Ύy=x2ΆΦœσ…œΘ§ΒΟΒΫyA=![]() Θ§yB=
Θ§yB=![]() Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®3Θ©…ηAΘ®mΘ§m2Θ©Θ§BΘ®nΘ§n2Θ©Θ°ΉςΗ®÷ζœΏΘ§÷ΛΟςΓςAEOΓΉΓςOFBΘ§ΒΟΒΫmn=©¹1Θ°‘ΌΝΣΝΔ÷±œΏmΘΚy=kx+b”κ≈ΉΈοœΏy=x2ΒΡΫβΈω ΫΘ§”…Ηυ”κœΒ ΐΙΊœΒΒΟΒΫΘΚmn=©¹bΘ§Υυ“‘b=1ΘΜ”…¥ΥΒΟΒΫODΓΔCDΒΡ≥ΛΕ»Θ§¥”ΕχΒΟΒΫPDΒΡ≥ΛΕ»ΘΜΉςΗ®÷ζœΏΘ§ΙΙ‘λRtΓςPDGΘ§”…Ι¥Ι…Ε®άμ«σ≥ωΒψPΒΡΉχ±ξΘ°

 ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗ
ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ‘ΎΗ’Η’±’ΡΜΒΡ2016»ΪΙζΓΑΝΫΜαΓ±Θ§Οώ…ζΜΑΧβ“ά»Μ «…γΜαΫΙΒψΘ§Ρ≥ –Φ«’ΏΈΣΝΥΝΥΫβΑΌ–’Ε‘ΓΑΝΫΜαΟώ…ζΜΑΧβΓ±ΒΡΨέΫΙΒψΘ§ΥφΜζΒς≤ιΝΥ≤ΩΖ÷ –ΟώΘ§≤ΔΕ‘Βς≤ιΫαΙϊΫχ––’ϊάμΘ°Μφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΆ≥ΦΤΆΦ±μΘ®≤ΜΆξ’ϊΘ©Θ° 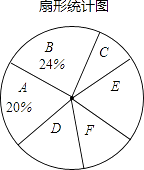
νl ΐΖ÷≤Φ±μ
Ήι±π | ΫΙΒψΜΑΧβ | ΤΒ ΐΘ®»Υ ΐΘ© |
A | “ΫΝΤΈά…ζ | 100 |
B | ≥ΤΖΑ≤»Ϊ | m |
C | ΫΧ”ΐΉΓΖΩ | 40 |
D | …γΜα±Θ’œ | 80 |
E | …ζΧ§ΜΖΨ≥ | n |
F | ΤδΥϊ | 60 |
«κΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΧνΩ’ΘΚm= Θ§ n= Θ° …»–ΈΆ≥ΦΤΆΦ÷–EΉιΘ§FΉιΥυ’ΦΒΡΑΌΖ÷±»Ζ÷±πΈΣΓΔ
Θ®2Θ©ΗΟ –œ÷”–»ΥΩΎ¥σ‘Φ800ΆρΘ§«κΡψΙάΦΤΤδ÷–ΙΊΉΔBΉιΜΑΧβΒΡ»Υ ΐΘΜ
Θ®3Θ©»τ‘Ύ’β¥ΈΫ” ήΒς≤ιΒΡ –Οώ÷–Θ§ΥφΜζ≥ι≤ι“Μ»ΥΘ§‘ρ¥Υ»ΥΙΊΉΔAΉιΜΑΧβΒΡΗ≈¬ «Εύ…ΌΘΩ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥ―ΓΑΈ―ß…ζ≤ΈΦ”ΓΑΚΚΉ÷Χΐ–¥¥σ»ϋΓ±Θ§Ε‘Ψ≈ΡξΦΕ“ΜΑύΓΔΕΰΑύΗς10Οϊ―ß…ζΫχ––ΚΚΉ÷Χΐ–¥≤β ‘Θ°ΦΤΖ÷≤…”Ο10Ζ÷÷ΤΘ®ΒΟΖ÷Ψυ»Γ’ϊ ΐΘ©Θ§≥…Φ®¥οΒΫ6Ζ÷Μρ6Ζ÷“‘…œΈΣΦΑΗώΘ§ΒΟΒΫ9Ζ÷ΈΣ”≈–ψΘ§≥…Φ®»γ±μ1Υυ ΨΘ§≤Δ÷ΤΉςΝΥ≥…Φ®Ζ÷Έω±μΘ®±μ2Θ©Θ°
±μ1
“ΜΑύ | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
ΕΰΑύ | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
±μ2
ΑύΦΕ | ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ | ΖΫ≤ν | ΦΑΗώ¬ | ”≈–ψ¬ |
“ΜΑύ | 7.6 | 8 | a | 3.82 | 70% | 30% |
ΕΰΑύ | b | 7.5 | 10 | 4.94 | 80% | 40% |
Θ®1Θ©‘Ύ±μ2÷–Θ§a= Θ§b= ΘΜ
Θ®2Θ©”–»ΥΥΒΕΰΑύΒΡΦΑΗώ¬ ΓΔ”≈–ψ¬ ΨυΗΏ”Ύ“ΜΑύΘ§Υυ“‘ΕΰΑύ±»“ΜΑύΚΟΘΜΒΪ“≤”–»Υ»œΈΣ“ΜΑύ≥…Φ®±»ΕΰΑύΚΟΘ§«κΡψΗχ≥ωΦα≥÷“ΜΑύ≥…Φ®ΚΟΒΡΝΫΧθάμ”…ΘΜ
Θ®3Θ©“ΜΑύΓΔΕΰΑύΜώ¬ζΖ÷ΒΡ÷–Ά§―ß–‘±πΖ÷±π «1Ρ–1≈°ΓΔ2Ρ–1≈°Θ§œ÷¥”’βΝΫΑύΜώ¬ζΖ÷ΒΡΆ§―ß÷–Ης≥ι1ΟϊΆ§―ß≤ΈΦ”ΓΑΚΚΉ÷Χΐ–¥¥σ»ϋΓ±Θ§”Ο ςΉ¥ΆΦΜρΝ–±μΖ®«σ≥ω«ΓΚΟ≥ιΒΫ1Ρ–1≈°ΝΫΈΜΆ§―ßΒΡΗ≈¬ Θ°