题目内容
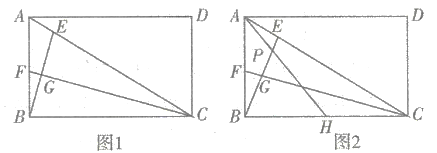
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为正方形的中心,点
为正方形的中心,点![]() 为
为![]() 边上一动点,直线
边上一动点,直线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,则
,则![]() 的最小值为( )
的最小值为( )

A.2B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
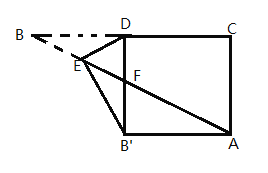
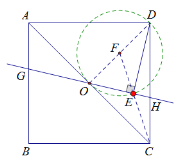
连接OD,AC,取OD中点F,由∠OED=90°可证得点E在以OD中点F为圆心,DF为半径的圆上,进而可知当点C、E、F三点在同一直线上时,CE取最小值,由正方形的性质可得OD=OC=2,进而可得OF=1,最后用勾股定理即可求得CF的长,进而可求得CE的最小值.
解:连接OD,AC,
由题意可知,在正方形中,OD⊥AC,
∵在△ODE中OD的长为定值,∠OED始终为90°,
∴点E在以OD中点F为圆心,OD为直径的圆上,
连接EF,CE,当点C、E、F三点在同一直线上时,CE取最小值,
∵正方形的边长为![]() ,点O为正方形中心,
,点O为正方形中心,
∴![]() ,
,
∴![]() ,
,
∴在Rt△ABC中,![]() ,
,
∴CE的最小值为![]()
故选:D.

练习册系列答案
相关题目
【题目】某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2本乙种笔记本共需29元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种比价本x本.
①填写下表:
甲种笔记本数量 | 10 |
|
乙种笔记本数量 |
| 30 |
所需总费用 |
|
|
②写出购买这两种笔记本所需要费用y(元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由