题目内容
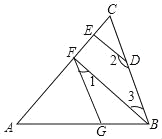
【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.
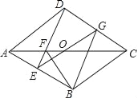
【答案】(1)见解析;(2)见解析.
【解析】
(1)首先证明△CBF≌△CDF,从而得到∠FBC=∠FDC,然后由平行线的性质可知∠FDC=∠AED,从而可证得∠AED=∠FBC;
(2)连接BD,由菱形的性质可知;OB=OD,然后再证明OG=OE,从而可证得四边形DEBG是平行四边形.
(1)∵四边形ABCD是菱形,
∴∠DCF=∠BCF,DC=BC.
在△DCF和△BCF中,
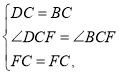
∴△DCF≌△BCF,
∴∠FBC=∠FDC.
∵DC∥AB,
∴∠FDC=∠AED.
∴∠AED=∠FBC.
(2)如图,连接BD.
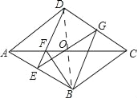
∵四边形ABCD是菱形,O是AC的中点,
∴OD=OB.
∵DC∥AB,
∴∠GCO=∠EAO.
在△GCO和△EAO中,
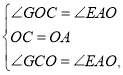
∴△GCO≌△EAO,
∴OE=OG.
∴四边形DEBG是平行四边形.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?