题目内容
【题目】根据下列证明过程填空:
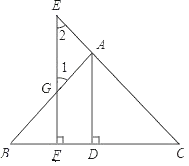
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴ = ( 两直线平行,内错角相等 ),
=∠CAD ( ).
∵ (已知),
∴ ,即AD平分∠BAC ( ).
【答案】平面内,垂直于同一条直线的两直线平行,∠1,∠BAD,∠2,两直线平行,同位角相等,∠1=∠2,∠BAD=∠CAD,角平分线定义.
【解析】试题分析:由AD⊥BC,EF⊥BC,可得AD∥EF,由两直线平行,内错角相等可得∠1=∠BAD,由两直线平行,同位角相等可得∠2=∠CAD,又因为∠1=∠2,所以∠BAD=∠CAD,即AD平分∠BAC.
试题解析:
证明:∵AD⊥BC,EF⊥BC,
∴∠ADC=∠EFC=90°,
∴AD∥EF(平面内,垂直于同一条直线的两直线平行),
∴∠1=∠BAD(两直线平行,内错角相等),
∠2=∠CAD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠BAD=∠CAD,即AD平分∠BAC(角平分线定义).

练习册系列答案
相关题目