��Ŀ����
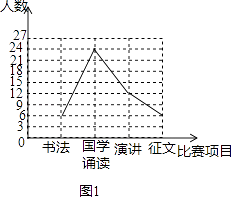
����Ŀ����Ԫ������֮�ʣ��ڷ���ѧ������¡�ص���ף�����Уͼ���չ�����鷨����ѧ�ж����ݽ��������ĸ�������Ŀ��ÿ��ֻ�μ�һ����Ŀ������ϣ���ࡱȫ��ͬѧ���μ��˱�����Ϊ�˽������ͬѧ�μӸ��������������ռ��������ݺ������²�����������ͳ��ͼ��ͼ1��������ͳ��ͼ��ͼ2��������ͼ���е���Ϣ������и��⣺ 
��1���������ϣ���ࡱȫ��������
��2���������ͳ��ͼ����������
��3�����������ֲμ��˱��������á��б���������״ͼ����������Dzμӵı�����Ŀ��ͬ�ĸ��ʣ�
���𰸡�
��1���⣺���ݽ�����12�ˣ�ռ25%��
��ţ�2��ȫ������Ϊ��12��25%=48���ˣ�
��2���⣺�߹�ѧ�ж�ռ50%��
���ѧ�ж�����Ϊ��48��50%=24���ˣ���
���鷨����Ϊ��48��24��12��6=6���ˣ���
��ȫ����ͳ��ͼ��
��3���⣺�ֱ���A��B��C��D��ʾ�鷨����ѧ�ж����ݽ������ģ�
����״ͼ�ã�
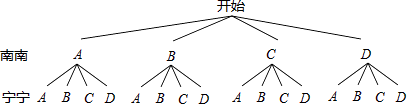
�߹���16�ֵȿ��ܵĽ�������Dzμӵı�����Ŀ��ͬ����4�������
�����Dzμӵı�����Ŀ��ͬ�ĸ���Ϊ�� ![]() =
= ![]()
����������1�����ݽ�����12�ˣ�ռ25%��������þţ�2��ȫ����������2����������鷨���ѧ�ж��������̶���ȫ����ͳ��ͼ����3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ�������Dzμӵı�����Ŀ��ͬ������������ø��ʹ�ʽ��⼴����ô𰸣�
�����㾫������������ͳ��ͼ������ͳ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ط�ӳ����ı仯��������Dz�������ر�ʾ������������ռ�İٷֱȣ�

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ����ͼ�٣��ѡϦ�=60���һ�����������γ���һ������ͼ�Σ����˻���ͼ�β��ϵĸ��Ʋ�ƽ�ƣ�ʹ����һ�����ε�һ��������ǰһ�����ε������غϣ������õ�ͼ�ڣ�ͼ�ۣ��� 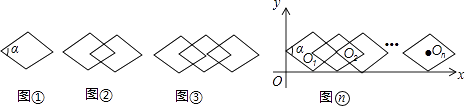
��1���۲�����ͼ�β�����±���
ͼ������ | ����ͼ�εĸ��� | ���εĸ��� |
ͼ�� | 1 | 1 |
ͼ�� | 2 | 3 |
ͼ�� | 3 | 7 |
ͼ�� | 4 | |
�� | �� | �� |
���룺��ͼ��n���У����εĸ���Ϊ���ú���n��n��3���Ĵ���ʽ��ʾ����
��2����ͼ����ͼ��n������ֱ������ϵ�У������е�һ������ͼ�ĶԳ�����O1������Ϊ��x1 �� 1������x1=����2017������ͼ�ε�����O2017������Ϊ ��