题目内容
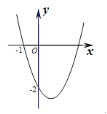
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.

(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)3;(2)B(-1,0);(3)D(2,3).
【解析】
试题(1)由二次函数![]() 的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
(2)根据(1)求得二次函数的解析式,然后将y=0代入函数解析式,即可求得点B的坐标;
(3)根据(2)中的函数解析式求得点C的坐标,由二次函数图象上有一点D(x,y)(其中x>0,y>0),可得点D在第一象限,又由![]() ,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
试题解析:(1)∵二次函数![]() 的图象与x轴的一个交点为A(3,0),∴
的图象与x轴的一个交点为A(3,0),∴![]() ,解得:
,解得:![]() ;
;
(2)∵二次函数的解析式为:![]() ,∴当
,∴当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,∴B(﹣1,0);
,∴B(﹣1,0);
(3)如图,连接BD、AD,过点D作DE⊥AB,∵当x=0时,y=3,∴C(0,3),若![]() ,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,
,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,![]() ,解得:x=0或x=2,∴点D的坐标为(2,3).
,解得:x=0或x=2,∴点D的坐标为(2,3).
另法:点D与点C关于x=1对称,故D(2,3).


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目