Question

【题目】如图，已知CE是Rt△ABC斜边AB上的高，在EC的延长线上任取一点P，连接AP，作BG⊥AP，垂足为G，交CE于D，求证：CE2＝PE·DE.

Answer 1

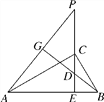
【答案】证明见解析

【解析】试题分析：

由已知易证△ACE∽△CBE，从而可得，即①；再证△AEP∽△DEB可得，即②；综合可得.

试题解析：

如图，

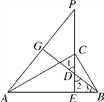
∵∠ACB＝90°，CE⊥AB，

∴∠ACE＋∠BCE＝90°，∠ACE＋∠CAE＝90°，

∴∠CAE＝∠BCE，

∴Rt△ACE∽Rt△CBE，

∴，

∴CE2＝AE·BE.

∵BG⊥AP，CE⊥AB，

∴∠DEB＝∠DGP＝∠PEA＝90°.

∵∠1＝∠2，

∴∠P＝∠3，

∴△AEP∽△DEB，

∴，

∴PE·DE＝AE·BE，

∴CE2＝PE·DE.