题目内容
【题目】如图所示，在四边形ABCD中，∠A=90°，AB=3，AD=4，BC=13，CD=12，求四边形ABCD的面积． 
【答案】解：连接BD
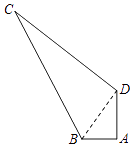
∵∠A=90°，AB=3，AD=4，
∴BD= 
=5．
∵在△BCD中，BD2+DC2=25+144=169=CB2，
∴△BCD是直角三角形，
∴S四边形ABCD= 
ABAD+ BDCD
= ×3×4+ ×5×12
=36．
故四边形ABCD的面积是36．
【解析】连接BD．先根据勾股定理求出BD的长度，再根据勾股定理的逆定理判断出△BCD的形状，再利用三角形的面积公式求解即可．
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
【题目】一次学科测验，学生得分均为整数，满分10分，成绩达到6分以上为合格．成绩达到9分为优秀．这次测验中甲乙两组学生成绩分布的条形统计图如下：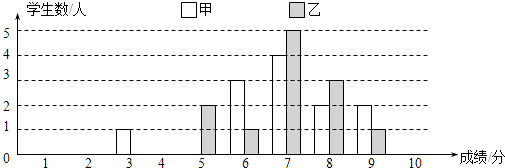
（1）请补充完成下面的成绩统计分析表：
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
（2）甲组学生说他们的合格率、优秀率均高于乙组，所以他们的成绩好于乙组．但乙组学生不同意甲组学生的说法，认为他们组的成绩要高于甲组．请你给出三条支持乙组学生观点的理由．
