题目内容
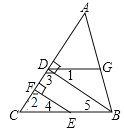
【题目】如图,BD⊥AC,EF⊥AC,D、F分别是垂足,且∠1=∠4,试说明:∠ADG=∠C.
【答案】说明见解析.
【解析】先由垂直的定义得到:∠2=∠3,然后由同位角相等,两直线平行得到:EF∥BD,再由两直线平行,同位角相等得到:∠4=∠5,然后根据等量代换得到:∠1=∠5,再根据内错角相等,两直线平行得到:DG∥BC,最后由两直线平行,同位角相等即可证∠ADG=∠C.
∵BD⊥AC,EF⊥AC(已知)
∴∠2=∠3=90° ( 垂直的定义),∴BD∥EF(同位角相等,两直线平行)
∴∠4=∠5(两直线平行,同位角相等)
∵∠1=∠4( 已知)
∴∠1=∠5(等量代换)
∴DG∥BC(内错角相等,两直线平行)
∴∠ADG=∠C( 两直线平行,同位角相等)

练习册系列答案
相关题目