题目内容
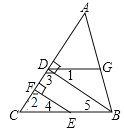
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
【答案】
(1)证明:∵∠AEF=90°,
∴∠FEC+∠AEB=90°;
在Rt△ABE中,∠AEB+∠BAE=90°,
∴∠BAE=∠FEC
(2)证明:∵G,E分别是正方形ABCD的边AB,BC的中点,
∴AG=GB=BE=EC,且∠AGE=180°﹣45°=135°;
又∵CF是∠DCH的平分线,
∴∠DCF=∠FCH=45°,
∠ECF=90°+45°=135°;
在△AGE和△ECF中, 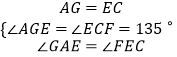 ;
;
∴△AGE≌△ECF;
(3)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,
∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,
∴BE= ![]() BC=
BC= ![]() AB=
AB= ![]() a,
a,
根据勾股定理得:AE= ![]() =
= ![]() a,
a,
∴S△AEF= ![]() a2.
a2.
【解析】(1)由于∠AEF是直角,则∠BAE和∠FEC同为∠AEB的余角,由此得证;(2)根据正方形的性质,易证得AG=EC,∠AGE=∠ECF=135°;再加(1)得出的相等角,可由ASA判定两个三角形全等;(3)在Rt△ABE中,根据勾股定理易求得AE2;由(2)的全等三角形知:AE=EF,即△AEF是等腰Rt△,因此其面积为AE2的一半,由此得解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目