Question

【题目】如图，在中，、两点分别在边、上，，与相交于点，若的面积为，则的面积为________．

Answer 1

【答案】

【解析】

根据等高的两个三角形底边的关系，可得两个三角形面积的关系，根据相似三角形判定与性质，可得AE：EG＝AF：FD＝3：4，根据比例的性质，可得AF：AD＝3：7，再根据等高的两个三角形底边的关系，可得两个三角形面积的关系．

如图，过D作DG∥BE，交AC与G，

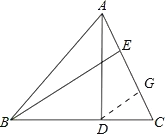
∵AE：EC＝CD：BD＝1：2，△ABC的面积为21，

∴S△ABE：S△BCE＝S△ADC：S△ABD＝1：2，

∴S△ABD＝S△ABC＝×21＝14，

∵DG∥BE，

∴△CDG∽△CBE，△AEF∽△AGD，

∴＝＝，

GE＝CE，AE＝CE，

AE：EG＝AF：FD＝3：4，

AF：AD＝3：7．

S△ABF：S△ABD＝3：7，

S△ABF＝＝37×14＝6，

故答案为：6．