题目内容
【题目】（发现）
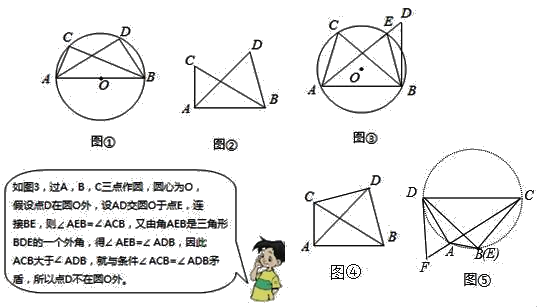
如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）．
如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？请证明点D也不在⊙O内．
（应用）
利用（发现）和（思考）中的结论解决问题：
（1）如图④，已知∠BCD=∠BAD，∠CAD=40°，求∠CBD的度数．
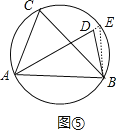
（2）如图⑤，若四边形ABCD中，∠CAD=90°，作∠CDF=90°，交CA延长线于F，点E在AB上，∠AED=∠ADF，CD=3，EC=2，求ED的长．
【答案】发现：点D也不在⊙O内；证明见解析；应用：（1）40°；（2）
.
【解析】
发现：如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上．如图⑤中，点假设D在⊙O内，延长AD交△ABC的外接圆于E，连接BE．利用反证法即可解决问题；
应用：（1）只要证明A、B、C、D四点共圆即可解决问题；
（2）只要证明点E与B重合，由∠DBC=∠DAC=90°，CD=3，BC=2，推出DE=DB=
=．
解：发现：如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上．
如图⑤中，点假设D在⊙O内，延长AD交△ABC的外接圆于E，连接BE．
∵∠ACB=∠AEB，∠ADB＞∠AEB，
∴∠ADB＞∠ACB，这个与已知条件∠ACB=∠ADB矛盾，
∴假设不成立，
∴点D也不在⊙O内．
应用（1）如图④中，
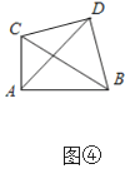
∵∠DCB=∠DAB，
∴A、B、C、D四点共圆，
∴∠CBD=∠CAD=40°，
（2）如图⑤中，
∵∠CDF=∠DAC=90°，
∴∠ADF+∠CDA=90°，∠CDA+∠ACD=90°，
∴∠ADF=∠ACD，
∵∠ADF=∠AED，
∴∠AED=∠ACD，
∵∠ACD=∠ABD，
∴点E与B重合，
∵∠DBC=∠DAC=90°，CD=3，BC=2，
∴DE=DB==．
