��Ŀ����
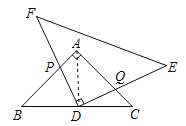
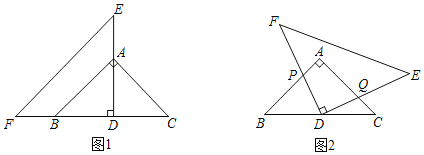
����Ŀ��������ֱ��������ABC��AB��AC����BAC��90�����͵���ֱ��������DEF��DE��DF����EDF��90������ͼ1�ڷţ���D��BC�ߵ��е��ϣ���A��DE�ϣ�
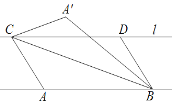
��1����գ�AB��EF��λ�ù�ϵ���� ����
��2����DEF�Ƶ�D��˳ʱ�뷽��ת����ͼ2��ʾλ��ʱ��DF��DE�ֱ�AB��AC�ڵ�P��Q����֤����BPD+��DQC��180����
��3����ͼ2������DEF�Ƶ�D��˳ʱ�뷽��ת�������У�ʼ�յ�P������A�㣬��ABC�������ΪS1���ı���APDQ�������ΪS2����ôS1��S2֮���Ƿ���ڲ����������ϵ�������ڣ���д������֮���������ϵ��֤�����������ڣ���˵�����ɣ�
���𰸡���1��ƽ�У���2������������3�����ڣ�S1��2S2�����ɼ�����.
��������
��1�����ݵ���ֱ�������ε����ʺ�ƽ���ߵ��ж��������ɵõ����ۣ�
��2�����ݵ���ֱ�������ε����ʵõ���B����C��45�㣬�ٸ��������ε��ڽǺͼ��ɵõ����ۣ�
��3������AD�����ݵ���ֱ�������ε����ʺ���ǵ����ʿɵ�BD��CD��AD����B����CAD����BDP����ADQ�������ɸ���ASA֤����BDP�ա�ADQ���ٸ���ȫ�������ε����ʼ��ɵõ����ۣ�
�⣺��1����AB��AC����BAC��90�������ABD����C=45����
��DE��DF����EDF��90�������F����E��45����
���F���� ABD����AB��EF��
�ʴ�Ϊ��ƽ�У�
��2����AB��AC����BAC��90�㣬���B����C��45�㣬
�ߡ�EDF��90�㣬���BDP+��CDQ��90�㣬
���BPD+��DQC��360�㩁��B����C����BDP����CDQ��180�㣻
��3��S1��S2֮����ڲ����������ϵ��S1��2S2.
���ɣ�����AD����ͼ����AB��AC��AD��BC��
��BD��CD��AD��![]() BC����B����C����CAD��45����
BC����B����C����CAD��45����
�ߡ�BDP+��ADP����ADP+��ADQ��90����
���BDP����ADQ��
���BDP�ա�ADQ��ASA����
��S��ABD��S��BPD+S��APD��S��ADQ+S��APD��S2��
�֡�S��ADB��![]() S1��
S1��
��S1��2S2��