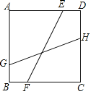
题目内容
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的点,
上的点,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 边上的点,连接
边上的点,连接![]() ,若线段
,若线段![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
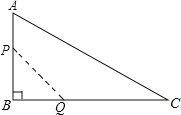
过点B作BK∥EF交AD于K,作BM∥GH交CD于M,可得∠KBM=45°,作∠MBN=45°交DC的延长线于N,求出∠ABK=∠CBN,然后利用“角边角”证明△ABK和△CBN全等,根据全等三角形对应边相等可得BN=BK,AK=CN,利用勾股定理列式求出AK,过点M作MP⊥BN于P,可得△BMP是等腰直角三角形,设GH=BM=x,表示出MP,然后利用∠N的正切值列出方程求解即可.
如图,过点B作BK∥EF交AD于K,作BM∥GH交CD于M,
则BK=EF=![]() ,BM=GH,
,BM=GH,
∵线段GH与EF的夹角为45°,
∴∠KBM=45°,
∴∠ABK+∠CBM=90°-45°=45°,
作∠MBN=45°交DC的延长线于N,
则∠CBN+∠CBM=45°,
∴∠ABK=∠CBN,
在△ABK和△CBN中,
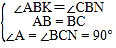 ,
,
∴△ABK≌△CBN(ASA),
∴BN=BK,AK=CN,
在Rt△ABK中,AK=![]() =1,
=1,
过点M作MP⊥BN于P,
∵∠MBN=45°,
∴△BMP是等腰直角三角形,
设GH=BM=x,则BP=MP=![]() BM=
BM=![]() x,
x,
∵tan∠N=![]() ,
,
∴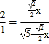 ,
,
解得x=![]() ,
,
所以GH=![]() ,
,
故选B.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目