题目内容
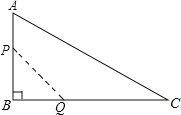
【题目】如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6![]() cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以
cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以![]() cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= (s);
(2)请你用含t的式子表示y.
【答案】(1)2;(2) .
.
【解析】
(1)由题意即可得出答案;
(2)当0≤t<2时,S△BPQ![]() BQBP,当2≤t时,如下图所示,S△BPQ
BQBP,当2≤t时,如下图所示,S△BPQ![]() BQHP即可求解.
BQHP即可求解.
解:(1)点P运动到点A,t=6×3=2(s).
故答案为:2.
(2)当0≤t<2时,y=S△BPQ![]() BQBP
BQBP![]() 3t
3t![]() t
t![]() t2,
t2,
即y![]() t2;
t2;
当t≥2时,作PH⊥BC于H,如图所示:

y=S△BPQ![]() BQHP
BQHP![]() t
t![]() (18﹣3t)
(18﹣3t)![]() t2
t2![]() t,
t,
即y![]() t2
t2![]() t.
t.

练习册系列答案
相关题目