��Ŀ����
����Ŀ��Ϊ�˸��ο��ṩ���õķ���ij��������Բ����οͽ����˹��ڡ���������������ȡ��ĵ��飬�����ݵ��������Ƴ����²�������ͳ��ͼ��.
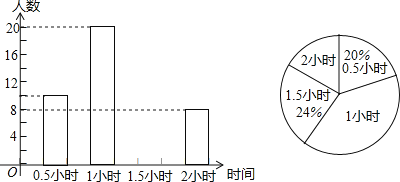
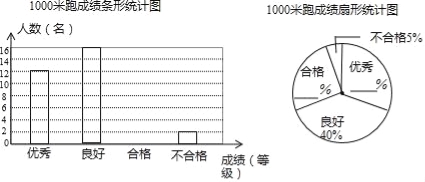
����� | ���� | ��ռ�ٷֱ� |
�dz����� | 12 | 10% |
���� | 54 | m |
�Ƚ����� | n | 40% |
������ | 6 | 5% |
����ͼ����Ϣ������������⣺
(1)���ε����������Ϊ______������m��ֵΪ_______��
(2)�벹ȫ����ͳ��ͼ��
(3)��ͳ�ƣ��þ���ƽ��ÿ��Ӵ��ο�Լ3600�ˣ��������dz����⡱�͡����⡱��Ϊ�οͶԾ����������Ŀ϶���������Ƹþ���������ƽ��ÿ��õ��������ο͵Ŀ϶�.
���𰸡�(1)120��45%��(2)��ͼ��������(3)ƽ��ÿ��õ�Լ1980�˵Ŀ϶�.
��������
��1���dz��������������ռ�ٷֱȼ��㼴�ɵã�����������������������ɵ�m
��2��������Ƚ������n��ֵ��Ȼ��ȫ����ͼ����
��3��ÿ��Ӵ����ο������dz�����+���⣩�İٷֱȼ���
��1��12��10%=120��54��120��100%=45%
��2���Ƚ����⣺120��40%=48(��)����ȫ����ͳ��ͼ��ͼ.

(3)3600����45%+10%��=1980(��).
�𣺸þ���������ƽ��ÿ��õ�Լ1980�˵Ŀ϶�.

 ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
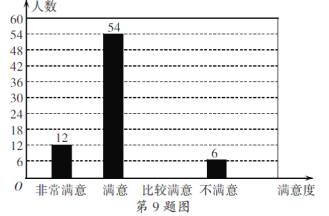
��ѧ�����ϵ�д�����Ŀ��������ѧ�����ʽ��������涨�����ʲ��Գɼ��ﵽ90.0�ּ����ϵ�Ϊ���㣻�ﵽ80.0����89.9�ֵ�Ϊ���ã��ﵽ60.0����79.9�ֵ�Ϊ����59.9�ּ�����Ϊ������ijУΪ���˽���꼶ѧ�����ʽ���״�����Ӹ�У���꼶ѧ���������ȡ��10%��ѧ���������ʲ��ԣ����Խ���������ͳ�Ʊ�������ͳ��ͼ��ʾ��
���ȼ�ѧ��ƽ����ͳ�Ʊ�
�ȼ� | ���� | ���� | ���� | ������ |
ƽ���� | 92.1 | 85.0 | 69.2 | 41.3 |
���ȼ�ѧ�������ֲ�����ͳ��ͼ

��1������ͳ��ͼ��������������ռ�İٷֱ��� ��;
��2����������ȡ��ѧ���IJ��Գɼ���ƽ���֣�
��3��������ȡ��ѧ�������в�����ȼ�ѧ�����ܷ�ǡ�õ���ijһ�����õȼ�ѧ���ķ���������Ƹþ��꼶ѧ����Լ�ж����˴ﵽ����ȼ���