题目内容
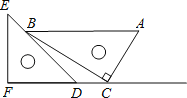
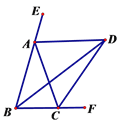
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.
以下结论:①AD∥BC; ②∠ACB=2∠ADB; ③∠ADC=90°-∠ABD; ④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有____________。(填写正确的序号)
∠BAC.其中正确的结论有____________。(填写正确的序号)
【答案】①②③⑤
【解析】分析:根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解析∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180,
∴∠ADC+∠ABD=90
∴∠ADC=90∠ABD,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=9012∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴⑤正确;
故填①②③⑤.