ЬтФПФкШн
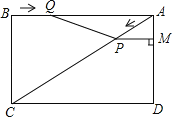
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкОиаЮABCDжаЃЌACЪЧЖдНЧЯпЃЌAB=4cmЃЌBC=3cmЃЎЕуPДгЕуAГіЗЂЃЌбиACЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЌЭЌЪБЃЌЕуQДгЕуBГіЗЂЃЌбиBAЗНЯђдШ
пFдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЌЙ§ЕуPзїPMЁЭADгкЕуMЃЌСЌНгPQЃЌЩшдЫЖЏЪБМфЮЊtЃЈsЃЉ
ЃЈ0ЃМtЃМ4ЃЉЃЎНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮPQAMЪЧОиаЮЃП
ЃЈ2ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙSЫФБпаЮPQAM=![]() SОиаЮABCDЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
SОиаЮABCDЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAPQгыЁїABCЯрЫЦЃП
ЁОД№АИЁПЃЈ1ЃЉЕБtЮЊ2![]() ЪБЃЌЫФБпаЮPQAMЪЧОиаЮЃЎ
ЪБЃЌЫФБпаЮPQAMЪЧОиаЮЃЎ
ЃЈ2ЃЉДцдкt=2ЃЌЪЙSЫФБпаЮPQAM=![]() SОиаЮABCDЃЎ
SОиаЮABCDЃЎ
ЃЈ3ЃЉЕБt=2![]() Лђ1
Лђ1![]() ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШИљОнЫФБпаЮABCDЪЧОиаЮЃЌЧѓГіACЕФГЄЖШЪЧЖрЩйЃЛШЛКѓИљОнЯрЫЦШ§НЧаЮХаЖЈЕФЗНЗЈЃЌХаЖЯГіЁїAPQЁзЁїACBЃЌМДПЩЭЦЕУ![]() ЃЌОнДЫЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
ЃЌОнДЫЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
ЃЈ2ЃЉДцдкt=2ЃЌЪЙSЫФБпаЮPQAM=![]() SОиаЮABCDЃЎЪзЯШИљОнЫФБпаЮABCDЪЧОиаЮЃЌЧѓГіSОиаЮABCDЕФжЕЪЧЖрЩйЃЛШЛКѓЗжБ№ЧѓГіЁїAPMЁЂЁїAPQЕФУцЛ§ИїЪЧЖрЩйЃЌдйИљОнSЫФБпаЮPQAM=
SОиаЮABCDЃЎЪзЯШИљОнЫФБпаЮABCDЪЧОиаЮЃЌЧѓГіSОиаЮABCDЕФжЕЪЧЖрЩйЃЛШЛКѓЗжБ№ЧѓГіЁїAPMЁЂЁїAPQЕФУцЛ§ИїЪЧЖрЩйЃЌдйИљОнSЫФБпаЮPQAM=![]() SОиаЮABCDЃЌЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
SОиаЮABCDЃЌЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
ЃЈ3ЃЉЕБt=2![]() Лђ1
Лђ1![]() ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎИљОнЬтвтЃЌЗжСНжжЧщПіЬжТлЃКЂйЕБЁЯAQP=90ЁуЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЛЂкЕБЁЯAPQ=90ЁуЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЛЧѓГіЕБtЮЊКЮжЕЪБЃЌЁїAPQгыЁїABCЯрЫЦМДПЩЃЎ
ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎИљОнЬтвтЃЌЗжСНжжЧщПіЬжТлЃКЂйЕБЁЯAQP=90ЁуЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЛЂкЕБЁЯAPQ=90ЁуЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЛЧѓГіЕБtЮЊКЮжЕЪБЃЌЁїAPQгыЁїABCЯрЫЦМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ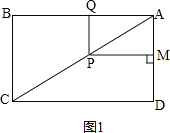 ЃЌ
ЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрAC=![]() =
=![]() =5ЃЌ
=5ЃЌ
ЁпЫФБпаЮPQAMЪЧОиаЮЃЌ
ЁрPQЁЭABЃЌ
гжЁпCBЁЭABЃЌ
ЁрPQЁЮCBЃЌ
ЁрЁїAPQЁзЁїACBЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУt=2![]() ЃЌ
ЃЌ
ЁрЕБtЮЊ2![]() ЪБЃЌЫФБпаЮPQAMЪЧОиаЮЃЎ
ЪБЃЌЫФБпаЮPQAMЪЧОиаЮЃЎ
ЃЈ2ЃЉДцдкt=2ЃЌЪЙSЫФБпаЮPQAM=![]() SОиаЮABCDЃЎ
SОиаЮABCDЃЎ
ШчЭМ2ЃЌ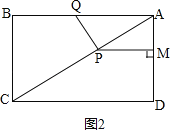 ЃЌ
ЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрSОиаЮABCD=ABBC=4ЁС3=12ЃЌ
ЁпPMЁЭADЃЌCDЁЭADЃЌ
ЁрPMЁЮCDЃЌ
ЁрЁїAPMЁзЁїACDЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУAM=![]() ЃЌPM=
ЃЌPM=![]() tЃЌ
tЃЌ
ЁрSЁїAPM=![]() AMPM=
AMPM=![]() ЁС
ЁС![]() =
=![]() t2ЃЎ
t2ЃЎ
ЁпsinЁЯPAQ=![]() =
=![]() ЃЌ
ЃЌ
ЁрSЁїAPQ=![]() APAQsinЁЯPAQ=
APAQsinЁЯPAQ=![]() tЃЈ4ЉtЃЉЁС
tЃЈ4ЉtЃЉЁС![]() =
=![]() tЃЈ4ЉtЃЉЃЌ
tЃЈ4ЉtЃЉЃЌ
ЁпSЫФБпаЮPQAM=![]() SОиаЮABCDЃЌ
SОиаЮABCDЃЌ
Ёр![]() t2+
t2+![]() tЃЈ4ЉtЃЉ=
tЃЈ4ЉtЃЉ=![]() ЁС
ЁС![]() ЃЌ
ЃЌ
ећРэЃЌПЩЕУ
t2Љ20t+36=0
НтЕУt=2Лђt=18ЃЈЩсШЅЃЉЃЌ
ЁрДцдкt=2ЃЌЪЙSЫФБпаЮPQAM=![]() SОиаЮABCDЃЎ
SОиаЮABCDЃЎ
ЃЈ3ЃЉЕБt=2![]() Лђ1
Лђ1![]() ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЂйгЩЃЈ1ЃЉЃЌПЩЕУ
ЕБt=2![]() ЪБЃЌЁЯAQP=90ЁуЃЌPQЁЮCBЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЪБЃЌЁЯAQP=90ЁуЃЌPQЁЮCBЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЂкШчЭМ3ЃЌ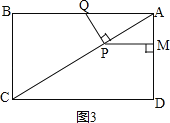 ЃЌ
ЃЌ
ЕБЁЯAPQ=90ЁуЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЌ
ЁпtanЁЯPAQ=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЁрPQ=![]() tЃЌ
tЃЌ
ЁпBQ=tЃЌ
ЁрAQ=4ЉtЃЌ
дкRtЁїAPQжаЃЌ
ЁпAP2+PQ2=AQ2ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУt=1![]() Лђt=Љ16ЃЈЩсШЅЃЉЃЎ
Лђt=Љ16ЃЈЩсШЅЃЉЃЎ
злЩЯЃЌПЩЕУ
ЕБt=2![]() Лђ1
Лђ1![]() ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ
ЪБЃЌЁїAPQгыЁїABCЯрЫЦЃЎ

 аЁбЇНЬВФШЋВтЯЕСаД№АИ
аЁбЇНЬВФШЋВтЯЕСаД№АИ аЁбЇЪ§бЇПкЫуЬтПЈЭбПкЖјГіЯЕСаД№АИ
аЁбЇЪ§бЇПкЫуЬтПЈЭбПкЖјГіЯЕСаД№АИ гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ
гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ