题目内容
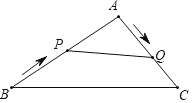
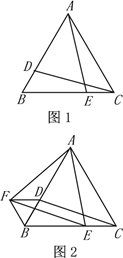
【题目】如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连结DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
【答案】(1)证明见解析;(2)①图中有2个正三角形,分别是△BDF,△AFE,证明见解析;②四边形CDFE是平行四边形,理由见解析.
【解析】(1)∵△ABC是正三角形,
∴BC=CA,∠B=∠ECA=60°. …………………………(2分)
又∵BD=CE,
∴△BCD≌△CAE. …………………………(3分)
∴CD=AE. …………………………(4分)
(2)① 图中有2个正三角形,分别是△BDF,△AFE. ……………………(6分)
由题设,有△ACE≌△ABF,
∴CE=BF,∠ECA=∠ABF=60° …………………………(7分)
又∵BD=CE,
∴BD=CE=BF,∴△BDF是正三角形, ………………………(8分)
∵AF=AE,∠FAE=60°,
∴△AFE是正三角形.
② 四边形CDFE是平行四边形. …………………………(9分)
∵∠FDB=∠ABC =60°
∴FD∥EC.
又∵FD=FB=EC,
∴四边形CDFE是平行四边形. …………………………(11分)
(1)易证△BCD≌△CAE,即可得出;(2)①可得出BD=BF,∠ABF=60°;AF=AE,∠FAE=60°,所以,图中有2个正三角形,分别是△BDF,△AFE;②可证得FD平行且等于EC,即可证得四边形CDFE是平行四边形.

 全优点练单元计划系列答案
全优点练单元计划系列答案