题目内容
【题目】如图,![]() 内的线段
内的线段![]() 、
、![]() 相交于点
相交于点![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 是__________.
是__________.

【答案】![]()
【解析】
连接AO,利用等高不等底的三角形面积比等于底边长的比,可表示出△AOC与△COD的面积.根据S△BOE+S△AOE=S△AOCS△COD,即可表示出四边形AEOD的面积.
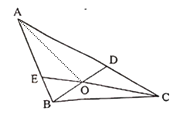
解:连接OA,设△BOE和△AOE的面积分别为m、n,
∴OC=2OE,
∴2S△BOE=S△BOC=2m,
∵OB=OD,
∴S△BOC=S△COD=2m,
∵OC=2OE,
∴2S△AOE=S△AOC=2n,
∵OB=OD,
∴S△AOB=S△AOD=m+n,
∴S△BOE+S△AOE=S△AOCS△COD,即:m+n=2n2m,
∴n=3m,
∵S四边形AEOD=S△AOE+S△AOD=n+m+n=m+2n=7m,
∴![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目