题目内容
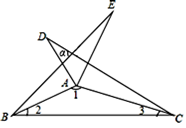
【题目】如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.
求证:△DEF是等腰三角形.
【答案】解:∵DG是EF边上的中线,EF=30cm,
∴EG=15cm,
∵DE=17cm,DG=8cm,
∴EG2+DG2=DE2 ,
∴DG⊥EF,
∴△DGE≌△DGF,
∴DE=DF,
∴△DEF是等腰三角形.
【解析】根据已知条件利用勾股定理求得DG⊥EF,又知EG=GF,可证明△DGE≌△DGF,所以可推出△DEF是等腰三角形.
【考点精析】关于本题考查的等腰三角形的判定和勾股定理的概念,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目