题目内容
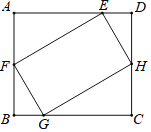
【题目】如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
【答案】①②④
【解析】
根据矩形的性质和同角的余角相等可判定①;根据AAS可判定②;先证△BFG∽△CGH,根据相似三角形的性质及勾股定理判定③;由③中求得的数据结合已知,根据矩形面积公式判定④.
∵∠FGH=90°,∴∠BGF+∠CGH=90°.
又∵∠CGH+∠CHG=90°,
∴∠BGF=∠CHG,故①正确.
同理可得∠DEH=∠CHG.
∴∠BGF=∠DEH.
又∵∠B=∠D=90°,FG=EH,
∴△BFG≌△DHE,故②正确.
同理可得△AFE≌△CHG.
∴AF=CH.
易得△BFG∽△CGH.
设GH、EF为a,
∴![]()
∴![]()
∴BF=![]()
∴AF=AB﹣BF=a﹣![]()
∴CH=AF=a﹣![]() .
.
在Rt△CGH中,
∵CG2+CH2=GH2,
∴32+(a﹣![]() )2=a2.解得a=2
)2=a2.解得a=2![]() .
.
∴GH=2![]() .
.
∴BF=a﹣![]() =
=![]() .
.
在Rt△BFG中,∵cos∠BFG=![]() =
=![]() ,∴∠BFG=30°.
,∴∠BFG=30°.
∴tan∠BFG=tan30°=![]() ,故③错误.
,故③错误.
矩形EFGH的面积=FG×GH=2×2![]() =4
=4![]() ,故④正确.
,故④正确.
故答案为:①②④

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
现将两组同学的测试成绩绘制成如下不完整的统计图表:
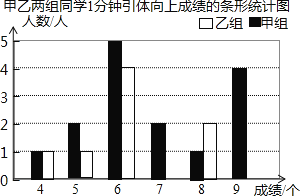
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.